Seeing in four dimensions

Three dimensions can be so limiting.

Mathematicians, freed in their imaginations from physical constraints, can conjure up descriptions of objects in many more dimensions than that. Points in a plane can be described with pairs of numbers, and points in space can be described with triples. Why not quadruples, or quintuples, or more?

There is the minor difficulty that our nervous systems are only equipped to conjure images in three dimensions. But that doesn’t stop Étienne Ghys of the École Normale Supérieure in Lyon, France, from visualizing the four-dimensional dynamical systems he studies: “I live in dimension four,” he says.

And you can too. Ghys has now created a series of video s teaching others to visualize four dimensions the way he does. His work is in collaboration with Jos Leys, a Belgian graphic artist and engineer, and Aurélien Alvarez, a mathematics graduate student at ENS Lyon.

The mathematician Ludwig Schläfli was one of the first to take higher-dimensional objects seriously, though he probably had little idea how to visualize them. In three dimensions, there are five regular solids, shapes for which every face is identical. In the mid-1800s, Schläfli figured out that in four dimensions, there are six regular solids, including one with 600 faces! Each of those 600 faces is itself a three-dimensional tetrahedron, and 20 of them meet at each vertex.

How on earth can we visualize such a thing? Ghys and his colleagues begin by pointing out that our challenge in visualizing four dimensions is very similar to the one that would be faced by a perfectly flat creature who lived in two dimensions and tried to visualize three, like the inhabitants of Edwin Abbott’s Flatland or the lizards in the page in Escher’s Reptiles . A cube or a sphere would be nearly unimaginable for the two-dimensional lizards, since they are unable to rise out of the plane.

Still, they could try. We depict three-dimensional objects on a page all the time, essentially by drawing their outlines. The lizards could develop some sense of three dimensions by examining these drawings. Multiple drawings from different perspectives might be especially helpful.

The lizards could also take another approach. Suppose a three-dimensional object were to move through their plane. They could watch the shape it makes as it goes and try to fit those shapes together into a sense of the whole.

Sadly, though, this method would turn out to be surprisingly difficult. Even for us, each with a lifetime of experience seeing three-dimensional objects, it can be hard to guess the three-dimensional shape from its two-dimensional cross-sections.

So the filmmakers offer the lizards a third method called “stereographic projection,” which is less intuitive but much more helpful. Take a three-dimensional object, say a tetrahedron, and imagine pumping it up with air until it forms a perfect sphere with lines on the surface showing where the edges of the tetrahedron were. Now imagine putting the tetrahedron-sphere on a table, making it transparent, and putting a light bulb at the “north pole.” The light would project patterns from the tetrahedron-sphere onto the surface of the table. The flat lizard could learn about the tetrahedron by studying these patterns. If the tetrahedron-sphere rolled around, the lizards could view the projection from different angles.

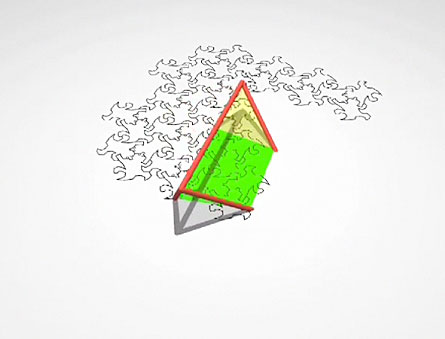
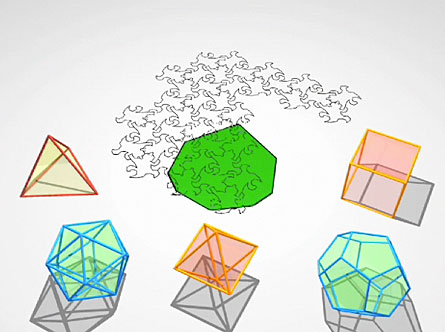
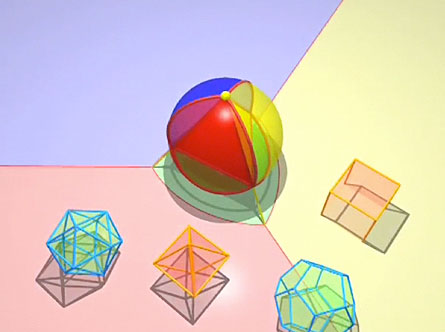
This method, it turns out, is remarkably easier. The tetrahedron outlines on the surface of the sphere are kept roughly the same when they’re projected, so its triangles are recognizable as three-sided shapes on the plane (though they’ve become rather curvy). This makes it far easier to imagine the three-dimensional object from its two-dimensional image.

So can any of these techniques help us visualize Schläfli’s 600-sided, four-dimensional shape? Using a computer, Ghys first passes Schläfli’s regular, four-dimensional shapes through three-dimensional space and looks at the three-dimensional “slices” created. This helps a bit, but just as in two dimensions, it’s not easy to assemble an image of the higher-dimensional shape this way.

Next, he draws the three-dimensional “shadows” of the four-dimensional objects. This turns out to be much better: Rotating the objects around to see different facets of them can give a pretty good feeling for their shapes.

Finally, he uses stereographic projection. The idea is the same as projecting from three to two: You blow the four-dimensional shape up into a ball, and then you place a light at the “north pole” and project the image down into three dimensions. That process is all-but-impossible for us to visualize, just as the process of projecting a three-dimensional ball would be impossible for the lizards to imagine. The results, though, are gloriously easy to make sense of.

Well, at least relatively so. “You have to practice,” Ghys says. “I’ve been thinking in dimension four for 30 years now.”

The videos are all available free at www.dimensions-math.org . The videos go on to show how we can visualize imaginary numbers geometrically, how fractal patterns emerge in the Mandelbrot set and Julia sets, and how beautiful and complex shapes can be built up from circles.