How can you tell if enough members of a terrorist cell have been captured or killed so there’s a high probability that the cell can no longer carry out an attack? A mathematical model of terrorist organizations might provide some clues. The question is what sort of mathematical model would work best.
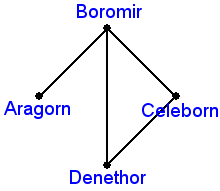
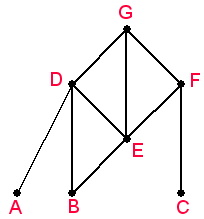
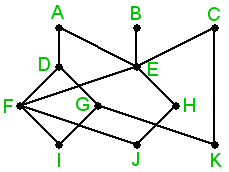
One way to describe a terrorist organization is in terms of a graph–a web of lines linking nodes. In this model, each node would represent an individual member of a given cell, and a line linking two nodes would indicate direct communication between those two members.
When a cell member is captured or killed, the corresponding node is removed from the graph. It’s possible to assess the impact of such losses on a cell’s effectiveness by considering how the links among the cell’s members are affected. Removing enough nodes leads to disruption.
Mathematically, you could ask the question: How many nodes must you remove from a given graph before it splits into two or more separate pieces?
For graphs of various sorts, it’s possible to estimate the probability that the removal of a certain number of nodes would split the graph into two or more separate units.
A graph model, however, may not be the best one available for representing a typical terrorist organization, mathematician Jonathan D. Farley of the Massachusetts Institute of Technology contends. He specializes in lattice theory and the theory of ordered sets.
“Our view is that modeling terrorist networks as graphs does not give us enough information to deal with the threat,” Farley wrote in a recent issue of Studies in Conflict and Terrorism. “Modeling terrorist cells as graphs ignores an important aspect of their structure, namely their hierarchy, and the fact that they are composed of leaders and followers.”
It’s not enough to disconnect terrorist networks, Farley argues. A remnant may yet contain a leader and enough followers to mount a serious attack.
Farley has proposed an alternative approach that better reflects an organization’s hierarchy. “My method uses order theory to quantify the degree to which a terrorist network is still able to function,” he says.
In this case, the relationship of one individual to another in a cell becomes important. Leaders are represented by the topmost nodes in a diagram of the ordered set representing a cell and foot soldiers are nodes at the bottom. Disrupting the organization would be equivalent to disrupting the chain of command, which allows orders to pass from leaders to foot soldiers.
A chain of command linking a leader with a foot soldier is called a maximal chain in the ordered set. A given ordered set may have several such chains. All of these chains must be broken for a cell (or remnant) to be considered ineffective.
Analyzing the structure and common nodes of such chains allows you to determine the probability that a terrorist cell has been disrupted. Farley has developed a formula for doing this calculation.
In general, Farley’s formula gives lower probabilities of success than those given by a simple graph model.
Farley suggests that his method of analysis could help officials make decisions about the allocation of resources, money, and personnel when fighting terrorism. “This tool will help law enforcement know when a battle against Al Qaeda has been won, thus saving the public’s money without unduly risking the public’s safety,” he says.
At the same time, Farley acknowledges that his “break the chains” model could be improved. It could be modified, for example, to reflect more complicated hierarchies, the dependence on rank of the likelihood of being captured, the effect of the passage of time, and other factors.
Farley’s model has several shortcomings. Law enforcement often doesn’t know how a terrorist cell is organized or even its full membership. It’s also not clear that terrorist attacks occur just when orders are passed down from leaders to foot soldiers.
Nonetheless, Farley contends, “this model enables law enforcement to plan its operations in less of an ad hoc fashion than they might be able to do otherwise.”






