You wouldn’t expect to learn much about the properties of water by watching a square dance. But think again. Following the caller’s lead, the dancers meet, separate, weave, and swing in a perfectly fluid manner.

It turns out that similar coordinated maneuvers—with water molecules taking the places of the dancers—may be responsible for some of water’s most puzzling features, an array of recent research findings suggest.
As liquids go, water is a radical nonconformist—differing from other liquids in dozens of ways (see the latest count at www.lsbu.ac.uk/water/anmlies). Most famous among water’s peculiarities is its density at low temperatures. While other liquids contract and get denser as they cool toward their freezing points, water stops contracting and starts to expand. That’s why ice floats and frozen pipes burst.
Water gets even weirder at colder temperatures, where it can exist as a liquid in a supercooled state well below its ordinary freezing point. Recent evidence suggests that supercooled water splits its personality into two distinct phases—another oddity unseen in other liquids. And last year, water surprised scientists yet again, when they found that at –63 degrees Celsius, supercooled water’s weird behavior returns to “normal.”
That discovery, scientists say, may help explain some aspects of water’s peculiar personality, such as its ability to transition from gas to liquid to solid and back to liquid again. Findings from related experiments have important implications for understanding how water interacts with biological molecules, such as proteins, and may lead to better ways of freezing and storing biological tissues such as sperm and human oocytes.
Plunging ahead
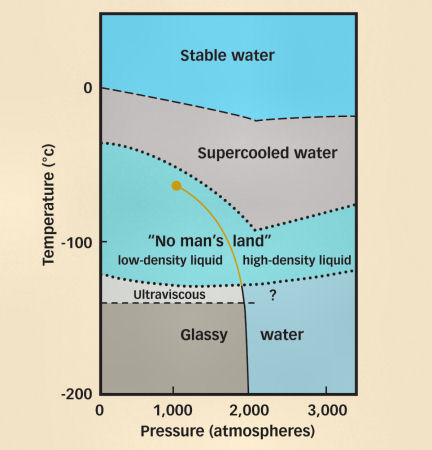
Water’s ability to exist in a liquid state well below its freezing point has been studied for centuries. What’s new, scientists say, is growing evidence about what happens to water at superlow temperatures. Under these extraordinary conditions, there is not just one kind of water, but two.
This two-phase phenomenon was first predicted in 1992 by physicist H. Eugene Stanley of Boston University and his graduate student Peter Poole, now at St. Francis Xavier University in Antigonish, Nova Scotia. Using computer simulations to study the behavior of liquid water at very low temperatures, the scientists suggested that water could exist as either a high-density liquid or as a low-density liquid.
Stanley and Poole also proposed that the dividing line between these two liquid forms might end in a “critical point,” where the two liquids would become indistinguishable, changing from one form to the other.
In a series of experiments in recent years, scientists have begun to close in on this critical point. These advances offer a glimpse of possible explanations for water’s unusual behaviors, and suggest that Stanley and Poole may have been on to something.
Molecular dance
Some of water’s odd properties have traditionally been explained as consequences of the hydrogen bonds that form between water molecules (and sometimes other molecules). Each V-shaped molecule of water contains one oxygen atom centered between two hydrogen atoms. The chemical bonds holding the molecule together create a slightly negative charge on the oxygen atom and a small positive charge on each of the hydrogen atoms.
These unequal charges make water molecules extremely “sociable”—eager to bond with each other. Because hydrogen bonds are much weaker than normal chemical bonds, the water molecules move about freely, binding briefly with adjacent molecules before moving on to others. Stanley likens this fast-paced network to a square dance taking place in a large dance hall.
“In square dancing, you’re always releasing one partner and grabbing another, and that is a hydrogen bond network, exactly,” he says.
In the case of water, the square dance occurs among molecules that have four arms, instead of two. That’s because each water molecule has the potential to form four hydrogen bonds. The result is a network of tetrahedrons, or pyramids with a triangular base.
This tetrahedral arrangement creates a peculiar tension, permitting structural changes in response to different temperatures and pressures. In liquid form, the tetrahedral structures allow unrestrained hydrogen bonding to occur as numerous molecules pack into and around the tetrahedron. (Imagine a swift square dance with dancers moving in and out of the center of the square and circling around it as well.) The result is a dense, fluid structure, such as that of everyday tap water.
As water approaches its freezing point (0°C), however, the tetrahedral structure becomes more open and begins to expand. Ordinary water reaches its maximum density at 4°C. As water continues to cool, falling to its freezing point and below, it continues to expand.
Here, the tetrahedral arrangement is more rigidly enforced, with molecules spaced an “arm’s length” apart. The arrangement creates a more spacious, open structure, and water becomes lighter. If ice weren’t lighter than cold water, ponds and lakes would freeze from the bottom, rather than form a floating layer of surface ice, and water would cease flowing in the dead of winter. Water’s weirdness therefore allows fish to swim in the water beneath the ice and plants to survive the winter cold.
At temperatures below the freezing point, ice crystals form around defects, such as cracks or dust particles. By using extremely clean water samples—free from any such defects—scientists have found ways to defy freezing and obtain supercooled liquid-water that remains liquid below 0°C.
This procedure works only to a certain point. At extremely cold temperatures, (–38°C and lower), it is nearly impossible to keep water from freezing. But under certain conditions, such as the ultrahigh pressures found deep undersea, water can remain liquid even at such low temperatures. Scientists have been unable to make water that cold in the laboratory, though, and so what Stanley calls a “no man’s land” of conditions had been explored only in computer simulations.
But now, using a clever technique to confine water samples in nanoscopic pores, scientists are beginning to explore the structure and properties of deeply supercooled water.
Terms of confinement
As even a square-dancing novice knows, you can’t hold a hoedown in a cramped, narrow hallway. Water’s hydrogen-bonding network is a fast-moving, gregarious one. Cramming water molecules into a tiny space, with a diameter less than five water molecules wide, brings the molecular square dance to a standstill.
“If a room were very, very narrow, it would be hard to have a normal square dance because a lot of people would be up against the wall and there would be no partner to grab on to,” Stanley says. “In a similar fashion, water molecules that are confined against a wall have only two or three arms, and the whole hydrogen-bond network is disrupted.”
Because the hydrogen-bond network brings stability to water, the breakdown of this network changes water’s properties, allowing it to remain liquid at a much lower temperature, he says.
Scientists began exploring ways to nanoconfine water molecules more than a decade ago, using a spongelike material that had holes of different sizes. While the experiments showed that nanoconfinement could be used to cool water well below its usual freezing temperature, the results were often hard to interpret because water in the larger holes would freeze, causing crystallization throughout the material.
In 2005, Sow-Hsin Chen of the Massachusetts Institute of Technology and his colleagues found a way to get around this problem, using a new material called MCM-41. Chung-Yuan Mou of National Taiwan University of Taipei had created MCM-41 by refining the fabrication of silica-nanotube assemblies. The material resembles a microscopic beehive with a hexagonal array of holes, all uniformly sized, just a few nanometers wide.
Curious to see how confined water might respond in MCM-41, Chen filled the hexagonal arrays with water. He then cooled the water to –73°C and bombarded the arrangement with neutrons. The microscopic cells of MCM-41 not only prevented ice crystals from forming but also allowed the scientists to probe water’s molecular structure.
Building on this work, Chen and colleagues conducted a series of experiments to see how water’s properties change as temperature drops at ordinary pressures.
In 2006, Chen showed that, when cooled below 225 kelvins (or –48°C), water’s hydrogen-bonding structure undergoes a phase transition, changing from a disordered, fluid state to a more ordered, rigid state. Furthermore, this line of transition between a high-density liquid and low-density liquid, called the Widom line, occurred in a continuous fashion, as predicted by Stanley and Poole in 1992. This transition, called a fragile-to-strong dynamic crossover, helped explain why, at superlow temperatures, proteins and other biological molecules exist in a glassy state, losing all flexibility and biological function.
“This dynamical transition of protein at 225 K is triggered by its association with the hydration water, which shows a similar dynamic transition at that temperature,” Chen says.
In addition, the study showed that water’s phase change at 225 K—moving from a disordered state to a more ordered state—violates a well-known formula called the Stokes-Einstein relation. This formula, based on a picture of a disordered, fluid state, ties together liquid properties such as diffusion, viscosity, and temperature, and generally works for normal- and high-temperature liquids.
Because this formula breaks down in subzero conditions, the experiment suggests that supercooled water may be a mix of two liquid phases, rather than a single liquid. Chen’s study, published in the Proceedings of the National Academy of Sciences (PNAS), provided the first experimental evidence of such “liquid polymorphism” and received the journal’s 2006 prize for best paper.
Last year, Chen and his colleagues surprised the scientific community, and themselves, when they discovered that under supercold conditions, liquid water again begins to expand, returning to normal behavior. Using a neutron-scattering method and analysis to measure the density of subzero liquid water, they showed that water reaches a minimum density at 210 K, or –63°C.
In doing the experiments, the scientists used heavy water, or D2O, because of its neutron-scattering properties. They then repeated the experiments using regular water and two light-scattering techniques and came up with the same results. The findings were reported last June in PNAS.
Though this kind of behavior had been predicted in computer simulations, it had never been observed. The findings add to the long list of experimental anomalies associated with supercooled water, and provide the strongest experimental evidence yet for a second “critical point” in liquid water, Chen says.
A critical point defines the set of pressures and temperatures at which a liquid changes from one form to the other. “It would be hard to explain a density minimum unless there was a second critical point,” he says.
Just a phase
Water already has one well-known critical point at 647 K, or 374°C, where, under ordinary pressures, the liquid and gas phases become identical.
“As water approaches this critical point, the difference between water and steam grows increasingly smaller,” Stanley explains. “At the critical point, there is nothing distinguishing water from steam, there is just one, homogeneous fluid.”
More important, he says, a critical point serves as a “tipping point,” where water can exist in either of two states, and minor fluctuations can tip the balance in one direction or the other.
The hypersensitivity created by a critical point can have far-reaching effects upon a system, says Stanley. In predicting a critical point in supercooled water, he and Poole theorized that water’s crazy low-temperature behavior might account for some of its unusual properties even at ordinary temperatures.
That’s because changes at a critical point don’t occur abruptly, Stanley says. The huge changes seen near the water-gas peak, for example, are often, if not always, foreshadowed by fluctuations over a large range of temperatures and pressures.
“It’s like looking at the highest peak on a mountain range,” Stanley says, gesturing toward a picture of Mount Everest in his office. “The critical point, or summit, doesn’t rise out of nowhere, but rises in a gradual manner and distorts the terrain all around it.”
That means that a critical point at –63°C might account for water’s bizarre behavior at much higher temperatures, such as its ability to expand as it cools.
Though findings from recent studies point to the predicted second critical point, it is still too soon to know whether such a point exists for sure. Further evidence is needed.
This year, Chen and his group will seek some of that evidence by performing another, more far-reaching set of experiments on supercooled water in MCM-41. Using a specially designed pressure cell for low temperatures, the scientists will analyze changes in liquid water as it moves from its maximum density point at 4°C to its minimum density at –63°C and beyond under various pressures. By studying how density changes with temperature and pressure, the researchers hope to locate the liquid-liquid critical point precisely.
“The critical point is at a high pressure, and no one knows exactly what it is, but we believe it’s probably above 1,000 atmospheres,” Stanley says.
Other scientists are raising questions about the extent to which supercooled water in confined volumes, no matter what the pressure, actually behaves like cold, bulk water.
“When you put water into confinement, it changes the way in which water molecules are arranged with respect to each other,” says C. Austen Angell, a chemist at Arizona State University in Tempe, who studies liquid phases in supercooled water. “The question is, how much does it change it?”
Angell notes that despite recent progress, much remains uncertain and many of the explanations are built on simulations that can give different results, depending on the model and tools used in the study.
“There are other possibilities, related to the second critical point scenario, in which the low-pressure supercooling of uncrystallized bulk water is terminated by a first-order [sharp] transition to a second ‘low-density’ liquid phase,” he says. Angell’s take on supercooled water will appear in an upcoming issue of Science.
Cold, hard facts
Confirming the predicted second critical point could have an impact beyond the study of water’s molecular mysteries for their own sake.
Biologists, for example, are looking at how this transition in liquid states, and the accompanying rigidity it brings, affects living structures such as proteins and DNA.
Other practical benefits could flow from the new water knowledge. For example, scientists at Cornell University have found that high-pressure cooling of protein crystals causes them to diffract better than they would if flash frozen, and has allowed scientists to improve methods for crystallizing and studying proteins and other biological tissues.
The scientists are now pursuing ways to use high-pressure techniques to improve methods for freezing sperm and human oocytes. The studies may lead to better ways of freezing and storing sperm for livestock production and allow women to freeze their eggs and use them at a later time to conceive a child.
The studies may also help explain some more ordinary, everyday occurrences related to water’s mysterious behavior. Chen recalls hiking in New Hampshire’s White Mountains, a site known for its frigid temperatures and long months of ice, and noticing that the trees stopped abruptly at 4,400 feet, nearly 2,000 feet below the summit of Mount Washington. Soon after he published his findings on a minimum density, he received a phone call from a Canadian biologist who was interested in the work.
“It turns out that this tree line stops where the windchill temperatures reach 220 degrees K,” Chen says, noting that this is the temperature at which water’s hydrogen-bonding structure undergoes a phase transition, changing from a fluid state to a more rigid state.
At this point water becomes very, very slow, and no longer supports biological functions. Or, to put it another way, the square dance of water comes to an end.
Susan Gaidos is a freelance writer in Maine.







