Swirling Seas, Crystal Balls

A field of triangles crumples and twists into a wavy crystalline sea. A crystal ball sprouts spiraling, labyrinthine passages. Faceted bricks stack snugly into a tidy, compact structure. Underlying each of these objects is a remarkable geometric shape made up of a sequence of triangles—a spiral polygon that resembles a seahorse’s tail.

Hungarian industrial designer and graphic artist Dániel Erdély called the form a spidron when he discovered it in the early 1970s. In so doing, he evoked the figure’s two spiral arms and the polygonal structures that can result when spidrons are joined.

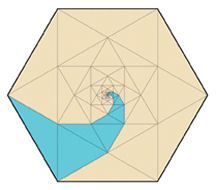
A standard spidron consists of two alternating, adjoining sequences of equilateral and isosceles triangles. Start with an equilateral triangle. Draw lines from the three corners of the triangle to a spot at its center, creating three identical isosceles triangles, each with angles of 30°, 120°, and 30°. Then, draw a reflection of one of these isosceles triangles so that it projects from the side of the original triangle.

Next, make a new equilateral triangle, using one of the two short sides of the jutting isosceles triangle as a base. Repeat the procedure again and again, producing a spiraling sequence of ever-smaller triangles. Erase the original equilateral triangle, and join two of these structures along the long side of the largest isosceles triangle to create the s-shape of a spidron.

Erdély observed that within each arm, the area of any equilateral triangle equals the sum of the areas of all the triangles with areas smaller than the given equilateral triangle. In other words, all the smaller triangles would fit together to fill the larger one.

Far more startling, however, is what happens when spidrons, laid down like tiles on a flat surface, are creased in just the right way and the flat, tiled structure is forced to fold accordion-style. The transformation from two to three dimensions creates mountain and valley folds that steepen. Each section of the pattern rotates as the configuration tightens. At its limit, it’s a wavy, three-dimensional surface made up of triangles at a few set angles to each other.

Sets of these creased and folded spidrons can themselves be assembled into a wide variety of intricate forms that resemble exotic crystal geodes.

“There’s a massive potential for sculpture here,” says artist Marc Pelletier, cofounder of the geometric-construction-kit company Zometool in Denver. “It’s really beautiful.”

Recent collaborations between Erdély and several artists and mathematicians have vastly increased the potential applications of spidrons, not only for creating intriguing art objects but also for engineering finely adjustable dynamic structures. For example, spidron reliefs could be used as shock absorbers or crumple zones in vehicles, Erdély says. Spidron surfaces could serve as flexible acoustic walls or solar panels. Spidron-based structures could also be used as blocks for builders—or construction toys.

Pelletier, his colleague Amina Buhler Allen, and math enthusiast Walt van Ballegooijen of the Netherlands have been working with Erdély for the past year, coming up with many new spidron-based designs. They presented their work in August in London at Bridges, a conference on mathematical connections among math, music, and art.

Hexagonal twist

Erdély started his spidron tinkering while working in a Budapest printing house, where he noticed networks of lines and hexagons on rolls of paper prepared for printing. Subsequent doodling beginning with a hexagon led him to an intriguing pattern. He had connected every second vertex of the hexagon with a straight line, thus creating a six-pointed star. Inside the star was a smaller hexagon. He again connected every second vertex and continued the process until the figure in the center was too small to distinguish. The resulting inscribed pattern consisted of just two types of triangles—equilateral and isosceles—that got smaller as they neared the hexagon’s center.

From his doodling, Erdély found that a hexagon contains six identical copies of a spiral sequence of triangles—a shape that he later called a spidron arm. His subsequent insight was to start with an array of inscribed hexagons drawn on a sheet of paper and laid as if they were bathroom tiles. By creasing the pattern in the right combination of mountains and valleys at the lines within each spidron arm and leaving a small hole at the center of each hexagon to allow movement, he crinkled the whole array into a dramatic three-dimensional relief.

In Erdély’s words, the folding pattern “mobilizes” the hexagonal array, permitting a flat surface to take on a range of three-dimensional forms. The surface area of the hexagon remains unchanged, and the constituent triangles neither bend nor distort.

In 1979, Erdély presented this swirling, moveable relief to his teacher, Ernö Rubik at the Hungarian University of Applied Art. According to Erdély, Rubik—known for the invention of Rubik’s cube—said that he’d never seen anything like it. That interest encouraged Erdély to continue experimenting with spidron structures.

Colored spidrons in various configurations make interesting tiling patterns on flat surfaces. Moreover, spidron patterns can be not only crinkled into reliefs but also assembled into novel three-dimensional crystal-like forms with spiral, polygonal faces.

But it wasn’t until after Erdély met Romanian crystal physicist Cristiana Grigorescu, that news of his discovery began to spread. Encouraged by Grigorescu, Erdély described spidrons in 1998 in Jerusalem at the 12th International Conference on Crystal Growth.

Five years later, mathematician Lajos Szilassi of the University of Szeged in Hungary provided the first mathematical description of Erdély’s spidron system and precisely defined its movements.

Subsequent collaborations with several artists, particularly Rinus Roelofs of the Netherlands, have vastly increased the realm of spidron structures and opened many new design possibilities. For example, Paul Gailiunas, an artist in Newcastle, England, encouraged Erdély to look for additional spidron-based polyhedral forms that can pack together to fill space.

The suggestion was fruitful. “[Erdély] has worked with many other people to create a wide variety of forms that I find visually and intellectually interesting,” Gailiunas says.

Gailiunas also urged Erdély to consider the possibility that spidrons might be constructed from parts of polygons other than hexagons. Now, the spidron originally discovered by Erdély is known to be one of a family of such figures.

“Since they found how to make spidrons based on other polygons, many more three-dimensional structures have become possible, and there is a lot still to explore,” Gailiunas says.

Pelletier is excited by the possibilities of what he describes as the “expanding spidron universe.” For example, he, van Ballegooijen, Buhler Allen, and Erdély have this year come up with various novel types of tilings, reliefs, and space-filling units, including ones that don’t have regularly repeating patterns. They’ve also used spidrons to construct many innovative three-dimensional forms—rings, nests, linkages, labyrinths, polyhedrons, and more. “We’ve increased what you can do with these things by an order of magnitude in just a few months,” Pelletier says.

Because spidrons are hinged, movable structures, they’re especially intriguing to artists and engineers, Gailiunas says. Many of the three-dimensional structures built from spidrons share this property.

“Modern computing techniques make it relatively easy to generate high-quality images and animations,” Gailiunas says. Erdély and his collaborators have generated “some really impressive material,” he adds. “And I’m sure there’s a lot more to come.”

---