Knotted threads secure buttons to shirts. Knots in ropes attach boats to piers. You can find knots in shoestrings, ties, ribbons, and bows. But even without Boy Scouts or sailors, knots would be everywhere.

Call it Murphy’s Law of knots: If something can get tangled up, it will. “Anything that’s long and flexible seems to somehow end up knotted,” says Andrew Belmonte, an applied mathematician at Pennsylvania State University in University Park. Belmonte has plenty of alarming anecdotal evidence. “It certainly happens in my house, with the cords of the venetian blind.” But the knot scourge is a global one, as anyone who owns a desktop computer can confirm after peeking at the mess of connection cables and power cords behind the desk.
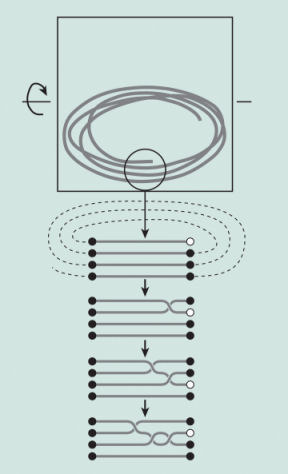
Now, scientists think they may have found out how and why things find their way into knotty arrangements. By tumbling a string of rope inside a box, biophysicists Dorian Raymer and Douglas Smith have discovered that knots—even complex knots—form surprisingly fast and often. The string first coils up, and then its free ends swivel around the other coils, tracing a random path among them. That essentially makes the coils into a braid, producing knots, the scientists say.
The results’ relevance may go well beyond explaining the epidemic of tangled venetian blind cords. That’s because spontaneous knots seem to be prevalent in nature, especially in biological molecules. For example, knottiness may be crucial to the workings of certain proteins (see “Knots in Proteins”). And knots can randomly form in DNA, hampering duplication or gene expression—so much so that living cells deploy special knot-chopping enzymes.
Raymer’s interest in knots began as an answer waiting for a question. Two years ago, he was an undergraduate student working in Smith’s lab at the University of California, San Diego (UCSD). Raymer fancied taking a class about the abstract theory of knots, offered by UCSD’s math department. Smith told him that he should take it only if he could find a practical use for it—some kind of knot experiment.
Raymer never took the class, but he and Smith did come up with a simple idea for an experiment. They put a string in a cubic container the size of a box of tissue. By tumbling the box 10 times “like a laundry dryer,” as Raymer puts it, the researchers hoped to observe knots forming spontaneously on occasion. They didn’t have to wait for long: Knots formed right away. “The first couple of times, it was pretty amazing,” Raymer says.
The researchers repeated the procedure more than 3,000 times, and knots formed about every other time. Longer strings, or more-flexible strings, tended to knot more often.
The researchers took pictures, planning to gather precise statistics of the types of knots that were forming. Raymer soon realized that, to make sense of the mess, he’d need to teach himself the mathematics of knots after all.
Ready-made tools
The theory of knots began in earnest in the 1860s, under the stimulus of the British physicist William Thomson, later known as Lord Kelvin. Kelvin suggested that atoms of different elements were really different kinds of knotted vortices in the ether. So to lay the foundations of chemistry, he believed, it was imperative to classify knots. Ultimately, physicists discovered that the ether didn’t exist. But mathematicians took an interest in knots for knots’ sake, as part of the young branch of mathematics called topology.
Topology studies shapes. Specifically, it studies shapes’ properties that are not affected by stretching, moving, twisting, or pulling—anything that doesn’t break up the object or fuse some of its parts. The proverbial example is that, to a topologist, a coffee mug is the same as a doughnut. In your imagination, you can squash the mug into a doughnut shape, and it will retain the property of having a hole, namely its handle.
A sphere is different. You can stretch a sphere into a stick and bend the stick so its ends touch. But turning that open ring into a doughnut will involve fusing the ends, and that’s forbidden.
In topology, a knot is any curved line that closes up on itself, possibly after a circuitous path in three dimensions. A circle is regarded as the “trivial” knot. Two loops are considered to be the same knot if you can turn one into the other by topological manipulation, which in this case means anything that does not break the curve or force it to run through itself.
Topologically, a knotted string is not a real knot, as long as its ends are free. That’s because either of the ends can always thread back through any entanglement and undo the knot. An open string, no matter how garbled, is the same as a straight segment. (Mathematicians usually think of strings as being stretchable and infinitesimally thin, so in topology there is no issue of a knot being tight.)
Strictly speaking, then, the string in Raymer and Smith’s box was never knotted. But it was still a mess. When the researchers joined the string’s ends, they made it into a closed loop, often something that even a mathematician would call a knot.
Raymer soon realized that telling different knots apart, or recognizing when two knots are the same is a tricky business. Topologists usually work with two-dimensional drawings of knots called knot projections. From different points of view, the same curve will look different and so will its projections. Topologists’ best tools for distinguishing knots are algebraic expressions called knot polynomials. These are sums of multiples of a variable, such as x, raised to different powers. The variable has no meaning per se, and all the information is in the numbers by which it’s multiplied. But the x‘s make it easier to calculate a knot polynomial starting from a knot projection.
James Alexander, a Princeton University mathematician, invented the first knot polynomial in the 1920s. Two topologically equivalent knots always will give the same Alexander polynomial, no matter how different their projections look. So if two knots have different polynomials, they’re certainly nonequivalent. The converse, however, is not true: Some distinct knots have the same Alexander polynomial. That means that the Alexander polynomial is not a fail-safe way of distinguishing knots.
In the early 1980s, Vaughan Jones of the University of California, Berkeley rekindled mathematicians’ interest in knots when he defined a new kind of knot polynomial, a discovery that earned him the Fields Medal, the most coveted prize in mathematics. The Jones polynomials distinguish knots with greater, if not complete, accuracy than the Alexander polynomials. That made the Jones polynomials Raymer’s choice to catalog his knots.
Tie land
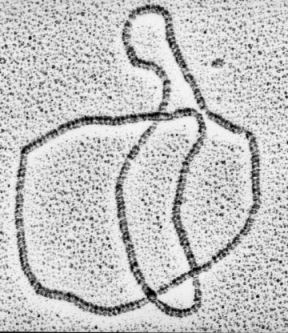
Raymer wrote a computer program to calculate Jones polynomials from the pictures he had taken each time he opened the box. The program found that the humble box had produced at least 120 distinct types of knots. Some were pretty complex.
The most basic measure of knot complexity is the minimal crossing number, the number of overpasses needed to draw the simplest possible projection of the knot. For the trivial knot, that number is zero. The simplest true knot, the trefoil requires that just three crossings be drawn. A few of the knots from the tumbling box required as many as 11, Raymer and Smith report in the Oct. 16 Proceedings of the National Academy of Sciences
Raymer says he and Smith were surprised, because previous knot experiments—physicists have tried a few in recent years—had seen only some of the simplest knots. For example, in 2001 Belmonte and his collaborators showed that a hanging chain (not from Belmonte’s venetian blinds) tended to knot up when shaken. In 2006, a team led by physicist Jens Eggers of the University of Bristol in England got a ball chain to form knots by setting it on a vibrating dish.
De Witt Sumners, an applied mathematician at Florida State University in Tallahassee, says he was not surprised that knots would form in a box. In computer simulations, mathematicians have found that random motion creates paths that almost always tie themselves up. Together with Stu Whittington of the University of Toronto, Sumners demonstrated mathematically in 1988 that if you wait long enough, these random walks will get knotted virtually 100 percent of the time.
Sumners suspects that with longer tumbling, Raymer and Smith would have gotten knots almost always, instead of just every other time. “They should have spun longer,” to see the full effects, Sumners says.
In their paper, on the other hand, Raymer and Smith propose a theoretical explanation for the mess in their box that differs from the most general type of random walk. Because their string tended to coil up whether or not it formed knots, they created a mathematical model of a bundle of coils as a series of parallel, horizontal strands. In a computer simulation, Raymer and Smith allowed one of the strands—representing one of the free ends of the string—to cross over or under one of the others in the bundle. After several such steps, the strands had braided, which often meant that the string as a whole was now knotted.
This simplified model didn’t reproduce the exact results of their experiment, but it did predict that specific knots had about the right odds of forming within the allowed time.
Jam-packed
Belmonte calls the braid model “very obvious, but maybe not universal,” meaning that different physical phenomena probably tie knots in different ways. In bacterial DNA, for example, one way that knots can form is by genetic recombination. That’s when, to facilitate the reshuffling of genes, enzymes cut DNA at two places and reattach the ends in a different order. Bacterial genomes are circular, so recombination can produce veritable knotted loops.
In the late 1990s, biochemists discovered enzymes that seem able to detect when DNA has a knot. The enzymes then undo the knot by brute-force cut and paste.
Keeping DNA tidy may be crucial to some of the cell’s most important functions. That’s because copying DNA and reading out the information it contains are performed by other enzymes, called polymerases, which walk along DNA. “When [a polymerase] comes to a knotted area, it will be stuck,” Belmonte says.
Scientists have discovered similar knot-busting enzymes in cells that have open-string chromosomes, such as in humans. The presence of such enzymes suggests that knotting may be an issue for human chromosomes as well. And scientists have also found knots in mitochondria, cellular organelles that contain loop DNA.
Another place where DNA knots can form is inside viruses, says Andrzej Stasiak, a structural biologist at the University of Lausanne in Switzerland. Viruses build containers called capsids in which the viruses tightly pack their DNA for traveling from one host cell to the next. In some viruses, the capsid keeps DNA at a pressure of more than 60 atmospheres.
Stasiak says that the packing process probably produces coiling similar to that seen by Raymer and Smith. Their coil-and-braid model could help explain why the DNA of some viruses often ends up being knotted.
But even if Raymer and Smith’s results don’t prove to be directly relevant to the molecules of life, they are “a very good beginning” for a general study of physical knots, according to Belmonte. “Now we can at least ask these questions: Are there universal laws of knots?”






