Many a mathematician has received a long letter from an unknown sender who claims to have found a way to trisect an angle using only a straightedge and compass. The mathematician may read passages of the letter aloud to the guffaws of colleagues at afternoon tea and then toss it out. Without even reading the details, any mathematician would know the writer is incorrect. In the early nineteenth century, the young French mathematician Évariste Galois proved the problem to be impossible.

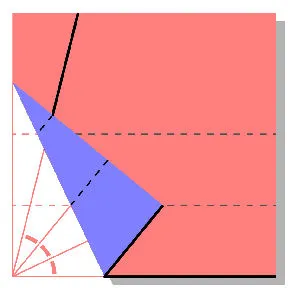
More recently, mathematicians have found that it is possible to divide an angle into three equal parts by folding paper rather than using a straightedge and compass.
Euclidean geometry is based on a set of axioms that he used to create figures and prove theorems involving those figures. These axioms allow one to create straight lines by connecting two points or by extending an existing line. They also allow one to create circles using a given straight line as the radius. Euclid’s lines are mathematical abstractions that can be represented in a drawing or diagram. Generating those diagrams involves the use of two tools: a straightedge and a compass.
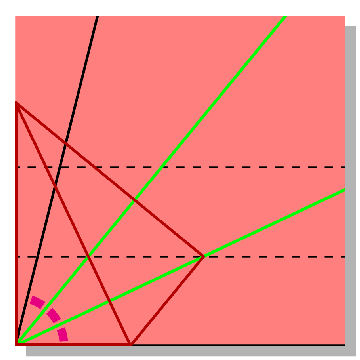
Origami artists create lines by folding paper instead of using a straightedge. Several mathematicians, including Humiaki Huzita of the University of Padua in Italy, have explored the range of figures one can create with origami folds. Huzita has codified origami folds into a set of six mathematical axioms for generating abstract lines. His axioms are analogous to Euclid’s. Five of them allow one to generate lines that Euclid could have drawn. The sixth axiom allows the creation of lines that Euclid would not have been able to generate.
The result is that origami artists can create any line that Euclid could have drawn, plus some additional lines. In particular, Hisashi Abe of Hokkaido University in Japan discovered how to use the non-Euclidean technique to generate lines that trisect any angle.
Bill Casselman of the University of British Columbia in Vancouver explains the technique in the May 2007 Notices of the American Mathematical Society. His article is based on Project Origami: Activities for Exploring Mathematics (2006, A.K. Peters Ltd.), a recent book by Thomas Hull of Merrimack College in North Andover, Mass.
Nevertheless, Galois’s theorem stands unmarred, and the letter-writers are incorrect. It remains impossible to trisect an angle using a straightedge-and-compass method. In fact, Hull also uses origami concepts in his book to illustrate Galois’s methods.
If you would like to comment on this article, please see the blog version.






