Here’s why we care about attempts to prove the Riemann hypothesis
The latest effort shines a spotlight on an enduring prime numbers mystery
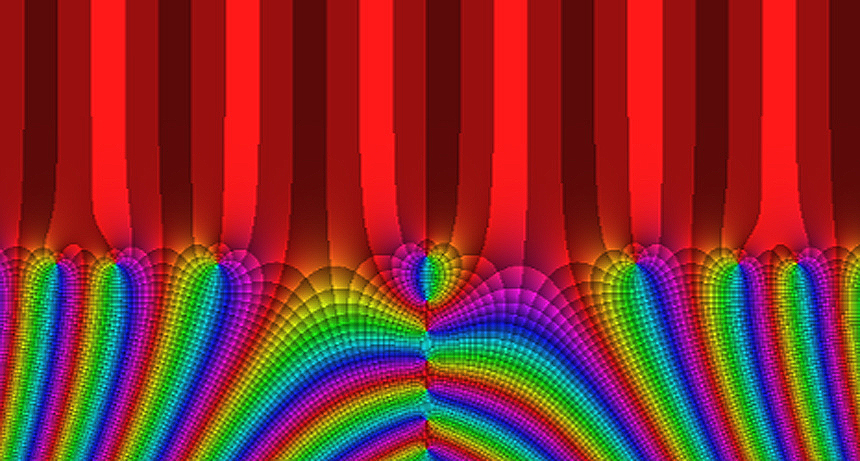
LINED UP The Riemann zeta function has an infinite number of points where the function’s value is zero, located at the whirls of color in this plot. The Riemann hypothesis predicts that certain zeros lie along a single line, which is horizontal in this image, where the colorful bands meet the red.
Empetrisor/Wikimedia Commons (CC BY-SA 4.0)