The simple mathematical concept of a pursuit curve can serve as the starting point for creating wonderfully intricate artistic designs.
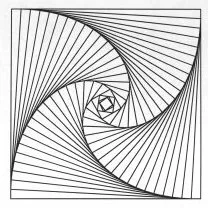



Pursuit curves can arise in a variety of situations. Suppose, for instance, that four bugs are at the corners of a square. They start to crawl clockwise at a constant rate, each moving toward its neighbor. At any instant, they mark the corners of a square. As the bugs get closer to the original square’s center, the new square they define rotates and diminishes in size. In reaching the center, each bug travels on a logarithmic spiral with a length equal to the side of the original square. Superimposed snapshots of the bugs’ progress add up to an intriguing pattern.
John Sharp of Watford, Herts, England, became interested in the artistic possibilities of pursuit curves in the late 1960s. He had studied chemistry at Oxford University and worked in industry as an analytical chemist for part of his career. He later wrote computer manuals. In school, Sharp also showed a talent for art. The fact that he is red-green color blind prompted an interest in optics and the psychology of vision.
These different threads came together for Sharp when he discovered the journal Scripta Mathematica, which highlighted cultural aspects of mathematics. Articles in Scripta Mathematica introduced Sharp to mathematical art and to so-called Op (for “optical”) art, particularly the work of illustrator and sculptor Rutherford Boyd (1882–1951). He also found inspiration in a 1968 exhibition called “Cybernetic Serendipity: The Computer and the Arts” at the Institute of Contemporary Art in London, where some early examples of computer-plotted pursuit curves were displayed. At that time, some of these designs even served as standard plotter test patterns.
In the 1970s, Sharp’s paintings reflected his interest in Op art and geometrical art. His purchase of an Apple II personal computer in 1979 provided him with the tool he needed to develop his mathematical art ideas further. Sharp’s explorations of pursuit curves and other mathematically inspired forms has continued to this day.
In the realm of pursuit curves, Sharp has investigated designs that arise when the standard rules are changed a little. For example, you can see what happens when bugs chase each other for several snapshots then reverse direction. Alternatively, you can start with bugs at the corners of a rectangle instead of a square (or, more generally, an irregular instead of a regular polygon). In the latter case, the nested polygons typically change shape, and the bugs fail to meet simultaneously at some central spot.
“The introduction of slight variations has opened a floodgate of new possibilities, with the addition of new illusions,” Sharp remarks. “Where overlaps occur. . ., the interplay of the lines gives rise to moire effects which enhance the design by giving the brain more to explore.”
“There are many more exciting possibilities if the pursuit takes place in three dimensions; for example, if the [bugs] become flies and start at the corners of polyhedra,” Sharp adds.
Computer programmer Bob Brill of Ann Arbor, Mich., is another artist who has been playing with pursuit curves for a long time. In a design called Lissajous Pursuit 2 (see http://users.migate.net/~bobbrill/Lp2.htm), he has just a single hound chasing a lone hare. The hare is constrained to hop along the path of a Lissajous figure. Starting at the figure’s center, the hound draws a bead on the hare and advances a certain distance along the straight line between the hound and the hare. The hare then hops to its next position, and the hound advances further along the new straight-line path to the hare.
“The algorithm ends when the hound catches the hare,” Brill notes. “Two parameters determine when this happens and ultimately what the image looks like: the distance advanced by each creature at each iteration of the process.”
The final image is made entirely of the straight lines drawn between hound and hare. “The wildly meandering curve, which is the path of the hound, is an emergent property of the algorithm, rising into visibility because the drawn straight lines are all tangent to this curve,” Brill notes.
In Buzzsaw Galaxy (see http://users.migate.net/~bobbrill/Buzzsaw.htm), the hound’s path is a spiral, and the hare hops along the perimeter of an ellipse. Brill has also created images in which the racing protagonists periodically reverse direction, vary their speeds or travel at different rates, and move under other constraints (for pursuit on the surface of a cube, see http://users.migate.net/~bobbrill/Algart.htm). “There are so many ways to pursue pursuits!” he concludes.
In the 1920s, Yale art historian Jay Hambidge (1867–1924) argued that design and great art can be created by the application of easily followed mathematical recipes. The art of pursuit curves is one manifestation of such mathematically inspired endeavors.






