It all started with Elvis.

![]()

In 2003, mathematician Tim Pennings of Hope College in Holland, Mich., revealed to the world that his Welsh corgi, Elvis, appears to be solving a calculus problem when finding the optimal path to fetch a ball. In this case, optimal path means minimizing travel time.
When Elvis and Pennings go to the beach, they always play fetch. Standing at the water’s edge, Pennings throws a tennis ball out into the waves, and Elvis eagerly retrieves it. When Pennings throws the ball at an angle to the shoreline, Elvis has several options. He can run along the beach until he is directly opposite the ball, then swim out to get it. Or he can plunge into the water right away and swim all the way to the ball. What happens most the time, however, is that Elvis runs part of the way along the beach, then swims out to the ball.
Depending on the dog’s running and swimming speeds, the strategy that Elvis follows appears to minimize the time that it takes to get to the ball. Indeed, Pennings found by experiment that Elvis performs in a way that closely matches a calculus-based mathematical model of the situation.
“It seems clear that in most cases Elvis chose a path that agreed remarkably closely with the optimal path,” Pennings argued in the May 2003 College Mathematics Journal.
Now, several other researchers have weighed in on the question of what sort of calculations dogs may do to reach their goals.
In the January College Mathematics Journal, Pierre Perruchet of the University of Bourgogne and Jorge Gallego of Robert-Debre Pediatric Hospital in Paris contend that the model chosen by Pennings assumes that the dog knows the entire route in advance in order to minimize the total duration of travel. Instead, they say, a dog optimizes its behavior on a moment-to-moment basis.
Perruchet and Gallego worked with a female Labrador named Salsa, who, like Elvis, apparently chooses the optimal path when playing fetch along a lakeside beach—in this case, near Nimes, France.
The researchers suggest that a dog playing fetch chooses at each point in time the path that allows it to maximize its speed of approach to the ball.
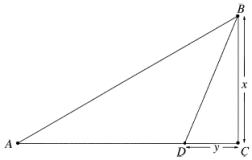
Here’s their argument. When running from A towards C, the ball at B appears closer and closer as the dog gets closer to C, but its speed of approach to B diminishes (reaching zero at C). At some moment of its run, its speed of approach while running on the beach equals its speed of approach when swimming directly to the ball. If the dog jumps into the water at this moment, the strategy yields the same y value as that provided by the travel-time minimization model (where r is the dog’s running speed, and s is its swimming speed).
“Although this solution is identical to that proposed by Pennings,” Perruchet and Gallego say, “it was gained without assuming canine knowledge of the entire route, and hence can be construed as a more plausible model for [the] dog’s strategy.”
However, for this alternative model to work, a dog must be able to estimate accurately its speed of approach at each moment and to have a general awareness of its swimming speed before entering the water. Perruchet and Gallego argue that dogs and other animals do have such motion detection capabilities.
On the other hand, Pennings insists that Elvis appears to make global decisions rather than instantaneous decisions when retrieving a ball.
The following experiment suggests why. “Playing fetch with Elvis, I decided to throw the stick while standing in the water, about 10-12 feet from shore, and with Elvis right beside me,” Pennings reports. “When I threw the stick in a path parallel to the beach, Elvis swam in to shore, ran along the beach for a sizeable distance, and then dove back into the water to retrieve the stick.”
“Thus,” he adds, “in swimming to shore he was not acting to minimize his distance to the stick as quickly as possible. Instead he did in fact apparently make a ‘global’ decision form the outset as to what path would get him to the stick most quickly.”
In the same issue of the College Mathematics Journal, mathematician Leonid Dickey of the University of Oklahoma proposes an extension—a strategy that dogs might use if they were initially not at the water’s edge but standing some distance from the shore. This becomes a problem in the calculus of variations.
Dickey then asks how a dog would respond if the soil properties (such as density and water content), and hence the running speed, changed gradually. But he presents no experiment data. Perhaps he doesn’t own a dog.
In the meantime, Elvis (full name Elvis Bogart Wales) has gone on to bigger and better things. A year ago, he was awarded an honorary degree “Litterarum Doctoris Caninarum” from Hope College. He even made a guest appearance in Keith Devlin’s new book, The Math Instinct: Why You’re a Mathematical Genius (Along with Lobsters, Birds, Cats, and Dogs).
Check out Ivars Peterson’s MathTrek blog at http://blog.sciencenews.org/.






