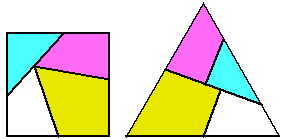
In recreational mathematics, a geometric dissection involves cutting a geometric figure into pieces that you can reassemble into another figure. For example, it’s possible to slice a square into four angular pieces that can be rearranged into an equilateral triangle.

Such puzzles have been around for thousands of years. The problem of dissecting two equal squares to form one larger square using four pieces dates back to at least the time of the Greek philosopher Plato (427 BC–347 BC). In the 10th century, Arabian mathematicians described several dissections in their commentaries on Euclid’s Elements. The 18th-century Chinese scholar Tai Chen presented an elegant dissection for approximating the value of pi–the ratio of a circle’s circumference to its diameter. Others worked out dissection proofs of the Pythagorean theorem. In the 19th century, dissection puzzles were an immensely popular staple of magazine and newspaper columns by puzzlists San Loyd in the United States and Henry E. Dudeney in England.
Dissections can get quite elaborate: A seven-pointed star becomes two heptagons; a dodecagon turns into three identical squares; and so on. You can also add constraints. For example, the pieces can be attached to one another by hinges. In the square-triangle dissection, the hinged pieces form a sort of chain. When closed in one direction, the pieces settle snugly into a square; when closed in the other direction, they fold into a triangle. (For an animated version of this dissection, see http://www.lsus.edu/sc/math/rmabry/live3d/hinged-triangle-square.htm.)
Now, chemists have gotten into the dissection game. As a novel strategy for getting small objects to assemble themselves into different regular forms, George M. Whitesides of Harvard University and his coworkers have developed a physical system that performs the same sorts of figure transformations that characterize dissection puzzles. The researchers describe their technique in the Dec. 11 Journal of the American Chemical Society.
The system consists of plates fabricated from plastic mixed with alumina powder and two immiscible liquids: water and an oily, dense substance called perfluorodecalin. With a density of 1.00 gram per cubic centimeter (g/cm3), water would float on top of perfluorodecalin, which has a density of 1.91 g/cm3. The plates, having a density of 1.65 g/cm3, would lie suspended at the interface between the two liquids.
The trick is to chemically treat each edge of a plate so that it is either water-attracting (hydrophilic) or water-repelling (hydrophobic). In general, like edges tend to attract and stick together via capillary forces. Plates can then spontaneously assemble themselves into larger aggregate structures.
When the plates float so that their centers of gravity are below the interface, water-attracting edges stick together. Increasing the density of water by adding a salt such as sodium metatungstate causes the plates to float higher. When their centers of gravity are above the interface, water-repelling edges stick together.
Carefully adjusting the density of the aqueous solution makes it possible to switch between different sets of edges to form different types of structures. In effect, which structure appears depends on the characteristics of the environment in which the plates find themselves.
Suppose, for example, that the plates are identical kite-shaped units. In one state, long edges stick together, so six plates collect to form a hexagon. In the other state, short edges attract, so three plates create an equilateral triangle, and these triangles assemble into a regular tiling.
It’s also possible to mimic the square-triangle transformation if the requisite plates are tethered together with thread so that they don’t drift apart or come together in the wrong order.
Of course, this chemical approach to dissections isn’t helpful for solving general dissection problems. You have to know the answers in advance to make it work. However, the technique does represent a flexible way of assembling small pieces into different types of arrays.






