Imagine a slick pebble that relentlessly drills its own hole as it drops toward Earth’s center, then continues onward. Affected only by Earth’s gravity and its rotation, what path would the frictionless pebble follow? How close to Earth’s center would it get?

These are among the intriguing questions that Andrew J. Simoson of King College in Bristol, Tenn., considers in an article in the June Mathematics Magazine.
“Deep holes elicit mystery,” Simoson writes. “For who among us when encountering a well with shadowed bottom is not tempted to drop a pebble and wait, listening for a splash?”
Indeed, the question of what happens to an object when dropped into a hole through Earth has a long history, in fiction and in the scientific literature. In 1632, Galileo Galilei (1564–1642) argued that a cannonball dropped down such a hole would oscillate forever between the drop site on one side of Earth and its putative exit site on Earth’s opposite side. The cannonball would exhibit simple harmonic motion.
In 1679, Isaac Newton (1643–1727) suggested that, in principle, observing the path that a falling ball follows as it descends such a hole would be one way to prove that Earth rotates. He speculated that a ball falling through a hole at the equator would follow a corkscrew trajectory.
For his analysis, Simoson assumes that a pebble is dropped at the equator of a rotating Earth whose density is spherically symmetric. He solves the differential equations that govern the pebble’s motion.
If Earth has the same density throughout, the mass acting gravitationally on a dropped pebble is proportional to the cube of its distance from Earth’s center. So, the gravitational force acting on the pebble is directly proportional to the distance. As an object travels toward Earth’s center, the gravity acting on it would decrease, until there’s no net gravitational force at the center itself.
As a result, a dropped pebble would follow an elliptical path in Earth’s equatorial plane, with Earth’s center at the ellipse’s center. The pebble would miss the center by more than 300 kilometers, and it would return to its drop point every 84.6 minutes.
What would the path look like to someone standing on Earth, which is itself in motion? In other words, Simoson asks, “what is the shape of a hole we must construct in the Earth so that a falling pebble never strikes the walls of the hole?”
It turns out that the geographical point where the pebble returns is actually about 2,360 kilometers due west of the geographical drop point, Simoson concludes.
Simoson then goes on to consider how an experiment involving a falling pebble could be used to measure Earth’s rotation. He also solves the pebble path problem for other gravitational fields.
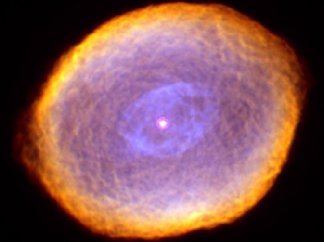
One particularly intriguing example involves a low-density, ellipsoidal cloud of matter encircling a small star, like that evident in the Spirograph Nebula.
In such a gravitational environment, Simoson says, it’s possible that chunks of matter “falling” through the Nebula would trace out paths in the form of spirographic swirls.
“Perhaps there are larger chunks of matter falling through the Nebula that behave as bulldozers or vacuum cleaners sweeping out channels in the clouds, somewhat like jets leaving trails in the sky or ocean liners leaving enormously long trails in the sea,” Simoson says.
He asks, “Is this gravitational phenomenon part of what helps to create the spirographic structure . . . , or is it just coincidence?”






