When a famous mathematician has something new to say, the whole world pays attention.

Euclid’s Elements, which presented the state of the art in geometry around 300 B.C., has been extraordinarily influential. This massive, 13-volume compendium set the standard for mathematical exposition and precise discourse for many centuries. More than 2,000 editions have been published, and new, interactive versions now appear on the World Wide Web.
What’s more, there is compelling evidence that Euclid of Alexandria (c. 365–275 B.C.) had a fourteenth book in mind. Officials of the Avril Foundation for Old Occidental Languages have announced that, after a year devoted to authentication and analysis, they are prepared to release the text of a manuscript that appears to be a Latin translation of research notes jotted down by Euclid in preparation for writing a fourteenth volume of Elements.
“This is truly an astonishing document,” says Duncan D. Umber of St. Patrick’s College of Medieval Studies, who recently examined the manuscript. “Euclid went much farther in his investigations than anyone had previously suspected. People continually underestimate what the ancients were able to do. We will need to reassess Greek mathematics in its entirety.”
The parchment manuscript was found by 12-year-old William Kelly, who was exploring a rocky cave on an island off the west coast of Ireland. At first, Kelly thought that he had discovered a treasure map. But the Latin words stymied him and the fanciful decorations reminded him of things he had seen in church. Kelly brought the packet to Seamus Donne, a local priest who happened to have an interest in illuminated manuscripts. Donne quickly appreciated the value of Kelly’s find and contacted the foundation.
The newly found work lacks the highly organized, compact structure of Elements. Its text refers to the definitions, axioms, and propositions contained in the first 13 books, but without the clarity and rigor of the preceding volumes. Obviously a work in progress, these pages document Euclid’s efforts to settle several important mathematical issues.
It’s clear that Euclid was uncomfortable with the fifth and most complicated of the five postulates that begin Elements. This postulate states, “If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than two right angles.”
Euclid’s newly discovered notes propose an alternative way of expressing this notion: “Through any given point can be drawn exactly one straight line parallel to a given straight line.” Euclid went on to consider two other cases: In one case, no parallel line can be drawn through the point, and in the other case, more than one parallel line can be drawn. In these two situations, he says, the sum of the interior angles of a triangle is no longer exactly equal to two right angles.
On the surface of a sphere, for example, the sum of the angles of any triangle is greater than two right angles, Euclid notes. Such a geometry has no parallel lines, yet it obeys his first four postulates.
The manuscript hints that Euclid also explored the curious geometry that arises from the existence of multiple parallels. “I have discovered things so wonderful that I was astounded,” he wrote at one point. “Out of nothing I have created a strange, new world.” Unfortunately, much of this section of the manuscript has deteriorated beyond repair, so only a few tantalizing fragments remain.
In another brief passage, Euclid mentioned a problem that he had had with determining the length of the coastline of a rugged island in the Aegean Sea owned by one of his former students. He observed that the answer obtained by a man pacing the island’s perimeter would differ from that of an ant making the same journey. The ant would take many more steps, following the shoreline’s ragged edge much more closely than the man would. A creature smaller than an ant would get an even larger estimate of the coastline’s length.
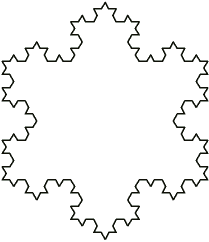
Euclid also shows how it’s possible to build a star-like figure out of triangles. He starts with a large equilateral triangle, then breaks up each side with a protruding equilateral triangle one-third as large. Then he repeats the procedure with each new side, adding successively smaller triangles. He calls the resulting shape an “asteroid.”
Euclid went on to speculate about how such self-similar forms may be useful for describing natural objects. “Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line,” he commented.
One highly cryptic section of Euclid’s notes refers to a massive computational project. He apparently had hundreds of students over a period of many years computing the squares of numbers, taking differences, and obtaining answers that served as starting points for successive steps in some kind of procedure for creating fanciful mosaics.
Euclid also spent time looking at extensions of the Pythagorean relationship (Proposition I.47). In his notes, he presented an ingenious argument to prove that the area of a right-angle triangle whose sides are all whole numbers cannot be a square of a whole number. Furthermore, he noted that it is impossible for a cube to be written as the sum of two cubes or a fourth power to be written as the sum of two fourth powers. Then he took a giant leap in conjecturing that the same thing holds for all powers greater than two.
Euclid left an intriguing note: “I have a truly marvelous demonstration of this proposition which this page is too small to contain.”
The remarkable material described in these long-lost writings reinforces the impression that, in Euclid’s time, the library at Alexandria in Egypt was much more than a reference institution or a school. It was also a major research center. Euclid’s Elements was intended not so much as a textbook but as a comprehensive accounting of what was known to date. It was meant to serve as a stepping stone toward new research in mathematics.
There are some skeptics. “Euclid was not a particularly brilliant mathematician,” says Bartholomew Cubbins of Banana Slug State University. “It’s wrong to credit him with these insights. I’m sure they were common knowledge in Euclid’s time, and he merely wrote them down.”
Nonetheless, the astonishingly wide range of these investigations and speculations means that our use of the term “non-Euclidean geometry” is clearly misleading. We can now honestly say that it’s all Euclidean geometry.
Check out Ivars Peterson’s MathTrek blog at http://blog.sciencenews.org/.






