
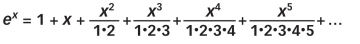
“Gentlemen, that is surely true, it is absolutely paradoxical; we cannot understand it, and we don’t know what it means. But we have proved it, and therefore we know it must be the truth.” —Benjamin Pierce, a Harvard mathematician, after proving Euler’s equation, eip = –1, in a 19th-century lecture.
Sunday, April 15, is the 300th birthday of Leonhard Euler (pronounced “oiler”), one of the most important mathematicians ever to have lived. His works help form the foundation of nearly all areas of mathematics, including calculus, number theory, geometry, and applied math.
One of the many discoveries for which he is famous is the equation eip = –1 . In a 1988 poll, readers of the journal Mathematical Intelligencer chose this equation as the single most beautiful equation in all of mathematics. The equation weaves together four seemingly unrelated mathematical numbers, e, p, i, and –1, in an astonishingly simple way.
But what does eip = –1 really mean?
First, let’s examine what the letters mean. The symbol e stands for a particular irrational number. Since it is irrational, its value can’t be given precisely in decimal notation, but it is approximately equal to 2.7183. Euler introduced this constant to the world of mathematics. He probably named it after the word “exponential,” because e is the base of the natural logarithms. Initially, he recognized the importance of e because of its remarkable properties in calculus. But e pops up over and over again in surprising places throughout mathematics. Somehow, this nearly magical number seems to tie the world together.
Pi, or p, is another irrational number. It rounds off to 3.14159, and it is defined as the ratio of the circumference of a circle to its diameter.
The “imaginary” number i is defined as the square root of –1. Imaginary numbers are unlike any number we encounter in ordinary experience. If i were an ordinary positive number, then multiplying it by itself would give a positive number, not –1. And if i were an ordinary negative number, then multiplying it by itself would also give a positive number, because multiplying a negative number by another negative number produces a positive number. Mathematicians therefore invented imaginary numbers, and they gave the name i to the square root of –1.
Cooking up new numbers might seem like a questionable proposition. But when a strange creation like i turns out to have remarkable and surprising properties, such as linking e to p in a simple equation, mathematicians are inclined to put aside any lingering qualms in favor of investigating what other secrets i might be hiding.
Imagining the imaginary
On inspection, eip is a peculiar concept. If the existence of an imaginary number seems strange, raising a real number to the power of an imaginary number is even odder. What could it possibly mean?
Euler found an answer to that question almost accidentally. He set out to understand functions, which are essentially mathematical machines that start with one number and produce another. Mathematical functions include x2 + 3x + 1, and sin x, and ex. Each of those formulas provides a method for starting with one number to produce another number.
Euler built on a remarkable discovery that mathematician Brook Taylor made in 1712. Taylor discovered that all types of mathematical functions, no matter how diverse they may seem, can be expressed in the same form, as a sum of powers of x.
When we apply Taylor’s method to the function ex, we get the following equation:
The right-hand side of the equation looks much more complicated than the left, but in fact it is much easier to calculate. The sums of powers of x, which we call polynomials, are the simplest kind of function in mathematics. In this case, the equation is a bit more complex than an ordinary polynomial because the sum continues infinitely. Nevertheless, expressing a function in this form allows mathematicians to understand it more clearly. Most importantly, the equation’s right-hand side doesn’t have any number raised to the power of x.
Taylor’s expansion offers a way to understand the complex and peculiar expression eip from Euler’s equation. That expression raises e to the power of i, which is a perplexing concept. But using the expanded form—the right side of Taylor’s equation—helps clarify matters.
Euler also faced the unfortunate fact that the Taylor expansion of eip continues infinitely. He solved that problem by comparing the Taylor expansion of eix with those of cos x and sin x. Those functions seem to be completely unrelated to ex, since they describe the relationships between the lengths of the sides of triangles. But Euler found the following remarkable identity:
eix = cos x + i sin x
When Euler set x equal to p, this equation made it easy to calculate the value of eip. The cosine of p equals –1, and the sine of p equals 0. So ein = (–1) + i (0). Therefore, eip = –1 + 0 = –1.
In honor of Euler’s birthday, we can all enjoy a birthday gift from him: Euler’s beautiful theorem.
Editor’s note: The character that appears as “p” on this page represents the Greek letter pi. In some browsers, it may not display properly.
If you would like to comment on this article, please see the blog version.






