Four friends move into a house and find they must choose among four rooms of different size and quality. Instead of sharing the rent equally, they decide to divide the total so that each person ends up satisfied with his or her combination of room and rent. Can they do it?
This is an issue that mathematics can settle, both elegantly and constructively, says mathematician Francis Edward Su of Harvey Mudd College in Clarement, Calif. Su has developed a new approach to the question of fair division and now offers an interactive Web site (http://www.math.hmc.edu/~su/fairdivision/) where people can go to resolve disputes over the splitting up of rent, goods, or even burdensome chores.
“My initial interest in this question was sparked by a friend who was actually facing [such a] dilemma,” Su remarks.
Aided by students Patrick Vinograd and Elisha Peterson, Su developed a Web-based “Fair Division Calculator.” It repeatedly queries each housemate in turn on which room he or she would prefer if the total rent were divided in certain ways among the rooms. A mathematical procedure, based on a combinatorial result known as Sperner’s lemma, determines room rents to propose after each housemate’s turn.
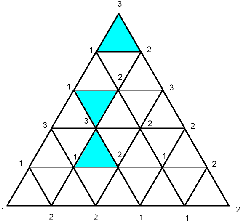
Sperner’s lemma concerns the labeling of geometric objects, such as triangles divided up into smaller (or elementary) triangles whose vertices are marked with 1s, 2s, and 3s. Those labels obey two conditions. The three vertices of the large triangle have different labels, and the label of a vertex of a smaller triangle along an edge of the larger triangle must match the label of one of the two vertices spanning that edge. Vertices of interior triangles can be labeled in any way.
Sperner’s lemma for triangles states that any Sperner-labeled triangulation must contain an odd number of elementary triangles possessing all labels. Indeed, there must be at least one such elementary triangle.
The same lemma can be extended to triangulations of n-dimensional triangles, or simplexes. Su takes advantage of this labeling result to work out a method of partitioning rent, where the labeling of vertices stands in for choices made by players.
After many interations, Su’s algorithm calculates an approximate solution that, in principle, everyone can live with. Occasionally, a player can end up with a negative rent–a monetary reward from the other players for putting up with an otherwise undesirable room. The scheme works for any number of participants.
Su continues to refine his methods. He now offers an option in which all the roommates enter bids on all the rooms. His mathematical algorithm then automatically works out a suggested rent allocation without the need for a string of queries.
Steven Brams of New York University and D. Marc Kilgour of Wilfrid Laurier University in Waterloo, Ontario, have proposed an alternative approach that works like an auction and avoids negative rents. The players bid competitively on the rooms available, but the player who bids highest for a particular room doesn’t necessarily get it.
Brams and Kilgour call their system the gap procedure. Assuming that the rent for a house is 100, each player bids on the rooms available so that his or her bids total 100. Rooms are assigned to different players so as to maximize the sum of the player bids.
Initially, this sum is greater than 100 (except in the case in which all the bids for each room are the same). The idea is to “descend” from this initial assignment to the next-lower bids for each room, and so on, until the sum of the current set of bids is less than or equal to 100.
Bids by Three Players for Three Rooms
| Room 1 | Room 2 | Room 3 | Total | |
| Player 1 | 50 | 1 | 49 | 100 |
| Player 2 | 29 | 40 | 31 | 100 |
| Player 3 | 31 | 38 | 31 | 100 |
In the example shown above, Player 1 is the high bidder for Rooms 1 and 3. The maximum sum is 121 (50 + 40 + 31), which happens to fall along the main diagonal in the table. The next-lower bids for the rooms are 31, 38, and 31. Because these bids sum to 100, no further steps are necessary. The bids become the room prices. Player 1 gets Room 1 for 31; Player 2 gets Room 2 for 38; and Player 3 gets Room 3 for 31.
According to this method, the price paid for a room depends not just on the winning bid but on lower bids as well. “Thereby, the market helps to set prices by incorporating the most competitive lower bids into the pricing mechanism,” Brams and Kilgour say. “It seems only fair that prices should be higher when there is greater demand for items.”
“What’s great about fair-division procedures,” Su contends, “is that no matter how other people behave, if you follow the procedure, you are guaranteed a share you think is fair.”






