The year 1202 saw the publication of one of the most famous and influential books in mathematics. Widely copied and imitated, Liber abaci introduced the use of Arabic numerals and the Hindu-Arabic place-valued decimal system into Europe. It was written by Leonardo Pisano, who became better known by his nickname Fibonacci.



A problem about proliferating rabbits in the third section of Liber abaci introduced what came to be termed the Fibonacci numbers: A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive?
The solution to the problem involves the following sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, and so on, where each number is the sum of the two preceding numbers.
You might expect some sort of tribute to Fibonacci in the city of Pisa in Italy, where he spent much of his adult life. That there is a dramatic artistic and mathematical tribute to Fibonacci in the town of Bowie, Maryland, on the outskirts of Washington, D.C., may come as a surprise, however.
Lake Fibonacci is a recently created reservoir at the Maryland Science and Technology Center, bordered by Curie Drive, Science Drive, and Melford Boulevard. The lake’s remarkable centerpiece is a massive, yet elegant fountain that spurts water as high as 36 feet into the air.
Created as a mathematical sculpture by artist and mathematician Helaman Ferguson, the fountain is made up of more than 45 tons of Texas granite, layered in alternating colors and rising to a height of 18 feet. It is supported by a concrete and steel platform atop pilings pounded 40 feet into the lake floor.
The fountain’s design embodies an intimate link between Fibonacci numbers and an irrational number known as the golden ratio, (1 + sqrt[5])/2, or 1.6180339887. . . . Ratios of successive terms of the Fibonacci sequence get closer and closer to the golden ratio. For example, the ratio 55/34 is 1.617647. . ., and the next ratio, 89/55, is 1.6181818. . ., and so on. Successive ratios alternate in overshooting and undershooting the golden ratio by decreasing amounts.
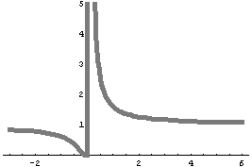
Ferguson based the profile of his fountain on a formula involving the golden ratio: f(x) = [(1 + sqrt[5])/2]1/x. Ignoring minus signs, thereby taking the absolute value, gives a two-part curve. As positive values of x get closer to zero, the value of f(x) shoots to infinity. As negative values of x get closer to 0, the value of f(x) gets closer to zero. Mathematicians describe the discontinuity at the value x = 0 as a singularity.
The 14 water cannons that fire spray into the air are located along the length (x axis) of the fountain at intervals proportional to the Fibonacci numbers.
Ferguson’s Fibonacci Fountain: Essential Singularity II owes its existence not just to the artist’s efforts but also to developer Dean Morehouse, who envisioned mathematical sculpture as an attractive feature in a business landscape. The lake itself has quickly become a home to ducks, turtles, fish, and other wildlife. Moreover, the fountain’s recirculating water brings oxygen into the lake, helping to keep it from stagnating.
The fountain presents varied vistas to those who take the 1-kilometer trek along Lake Fibonacci’s shoreline. At night, the shimmering play of water and light adds to the mathemagical effect.






