One of the most famous stories about Archimedes of Syracuse (287–212 B.C.) involves a bathtub. As recounted by the Roman architect Vitruvius (90–20 B.C.), the tale has Archimedes pondering the problem of determining the volume of a sacred wreath. The wreath was supposedly made of pure gold, and Archimedes had to determine whether the goldsmith had replaced some of the gold with silver.


While thinking about the problem, Archimedes happened to go to a bathhouse. As he was sitting down in the tub, he noticed that the amount of water that spilled out of the full tub was equal to the amount by which his body was immersed. According to Vitruvius, Archimedes was so delighted with his discovery and its role in solving the wreath problem that he ran naked through the streets toward his home, repeatedly shouting, “Eureka, eureka!”
In his book Archimedes: What Did He Do Besides Cry Eureka?, Sherman Stein of the University of California, Davis comments, “I doubt that such an elementary observation would have impressed Archimedes enough to stage a celebration, especially when it is compared to his dazzling discoveries about the surface area and volume of a sphere, the center of gravity, and the stability of floating objects.”
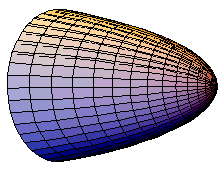
The fact that Archimedes was fascinated by floating bodies—perhaps inspired by experiences in the bathtub, observing ships in the harbor, or simply seeing debris floating in streams—is evident in two books that he wrote devoted to the topic. The second volume of On Floating Bodies, in particular, presents a sophisticated, detailed mathematical analysis of how a three-dimensional geometric form known as a paraboloid would float.
A paraboloid is a solid, cone-shaped object with a rounded nose and a flat base (above). Its base is either circular or elliptic, and a cross section at right angles to the base has the form of a parabola. When the base is at right angles to the axis of symmetry, the shape is called a right paraboloid.
In Book II of On Floating Bodies, Archimedes investigated the floating positions of a right paraboloid, searching for stable orientations of the form when it’s partially submerged in water.
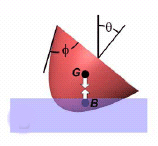
Two factors determine the way in which the paraboloid floats: its shape (the ratio of its height to the radius of its circular base) and its density (specific gravity).
Archimedes restricted his analysis to the case when a paraboloid’s flat base lies entirely above or entirely below the water surface. Now, mathematician Chris Rorres of the University of Pennsylvania has filled in the remaining cases, computing all possible floating positions (both stable and unstable) of a paraboloid for all possible shapes and densities.
“I wanted to show how ideas formulated millennia ago can come to life and yield new results with the use of modern computing and visualization tools,” Rorres says. He describes his findings in the current Mathematical Intelligencer.
The results obtained by Rorres reveal that interesting things happen when the base of a paraboloid is partially submerged in water. That’s precisely the situation that Archimedes couldn’t study with the mathematical tools available to him, Rorres says.
Rorres has posted illustrations and animations of his results on floating paraboloids at http://www.math.nyu.edu/~crorres/Archimedes/Floating/floating.html.
One intriguing situation involves a paraboloid with a relative density of 0.9. Initially, the largely submerged paraboloid is stable with its pointed end extending straight downward. However, as the paraboloid becomes narrower, it tilts, then abruptly tumbles onto its side.
Icebergs are known to be unstable and can tumble over for no apparent reason. Rorres’s paraboloid model suggests that, if an iceberg with a roughly paraboloidal shape melts so that it gets narrower, the block of ice can suddenly tip over once the height-to-radius ratio reaches a critical value and its base dips into the water.
A paraboloid with a very low relative density will float with its base parallel to and just below the fluid surface. As the relative density increases, the paraboloid sinks into the liquid, then begins to tilt. At a critical density and tilt angle, its base becomes only partially submerged, and the paraboloid topples onto its side.
Rorres likens this behavior to that of a tall building standing on water-saturated soil. During an earthquake, such soil can behave like a thick liquid. Structures originally supported by the soil begin to float. As the soil liquefies and its density decreases, the structure would sink, eventually exposing its base, then fall over.
“As with the iceberg, the paraboloidal structure cannot topple until its base is partially exposed above the soil level,” Rorres says. To fall over, the structure also has to be sufficiently narrow. For a wide base, a paraboloidal structure gradually sinks and tilts into the soil without toppling as the soil’s density decreases.
“No doubt Archimedes would have been interested in seeing the results of this paper,” Rorres writes, though Archimedes would have had to learn some new mathematics, such as the intricacies of three-dimensional Cartesian coordinate systems, to understand the work.
Archimedes “could . . . then appreciate some of the advances made in mathematics in the last 23 centuries,” Rorres adds, “although my guess is that he would have expected more, considering the enormous advances that he alone made in his lifetime.”
Puzzle of the Week
Sarah checks out the odometer on her car. It reads 14,941 miles. She notices that it reads the same backward as forward. “I wonder how long it will be before that happens again?” Sarah thought to herself.
To her surprise, in 2 hours the odometer showed a new palindrome number. What was the number, and what was the average speed of the car in those 2 hours?
For the answer, go to http://www.sciencenewsforkids.org/articles/20030820/PuzzleZone.asp.






