One of the treats of holidays long past was an activity that involved folding, then cutting a sheet or strip of paper to reveal a lacy snowflake or a chain of identical spruce trees, connected at their sides so it looked like branches brushing up against each other. The result was invariably a delightful surprise.
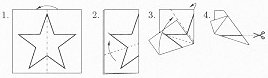
Accordion folds and judicious cutting can produce a string of paper dolls or a variety of geometric patterns. Instructions are available for creating a five-pointed star, any letter of the alphabet, various crosses and polygons, and even complex patterns, such as a star within a star. In some cases, both the snipped sheet and the “hole” represent desired forms.
This activity also suggests a mathematical question. Suppose you are limited to figures bounded by straight lines (polygons) and you are allowed only one straight cut. Using a fold-and-cut process, what shapes can you produce?
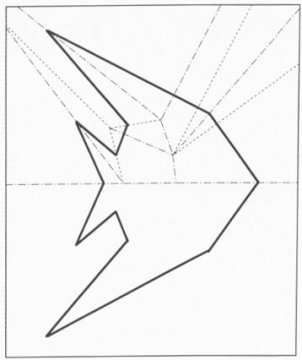
Remarkably, it turns out that, after an appropriate sequence of folds, any straight-line drawing (polygonal shape) can be cut out of one sheet of paper by a single straight cut. In other words, one cut suffices–whether the drawing consists of a single polygon, adjoining polygons, nested polygons, or an array of disjoint polygons.
Thanks to Erik D. Demaine and Martin L. Demaine of the Massachusetts Institute of Technology and Anna Lubiw of the University of Waterloo, this statement now has the power of a theorem. Indeed, Demaine and his colleagues developed a systematic procedure that, for a given target shape, shows how the original sheet must be folded then cut to achieve the desired result.
This algorithm generates folds based on a structure known as the straight skeleton. Roughly speaking, for each face (the area between cuts) of the desired pattern, shrink the face so that its edges stay parallel and move at a constant speed in a perpendicular direction. Stop whenever the boundary intersects itself and continue shrinking each piece. The straight skeleton consists of the paths of the vertices of the desired cut pattern during this shrinking process. It has the effect of lining up the desired edges by folding along various bisectors. An additional collection of perpendiculars makes the full crease pattern foldable.
Erik Demaine, Marshall Bern of the Xerox Palo Alto Research Center, David Eppstein of the University of California, Irvine, and Barry Hayes of Placeware later worked out an alternative algorithm–based on disk packing–for solving the fold-and-cut problem.
“These algorithms,” Erik and Martin Demaine remark, “allow us to design many practical examples of the fold-and-cut idea that go far beyond what was previously possible.”






