The Geometry of Music

The connection between mathematics and music is often touted in awed, mysterious tones, but it is grounded in hard-headed science. For example, mathematical principles underlie the organization of Western music into 12-note scales. And even a beginning piano student encounters geometry in the “circle of fifths” when learning the fundamentals of music theory.

But according to Dmitri Tymoczko, a composer and music theorist at Princeton University, these well-known connections reveal only a few threads of the hefty rope that binds music and math. To grasp the true structure of music, he says, we need to understand the geometry of hyperdimensional objects. Doing so has given him new ways of understanding pieces of music that have long baffled theorists and even led him to new insights into the history of music.

Tymoczko compares the structure of music to the shape of a rock face that a rock-climber is scrambling up. “If you know the conditions of the rock face, you can predict the motions of the climber,” he says. “The structure of the space makes certain choices overwhelmingly natural or convenient. There’s something similar that goes on with music. When you think about things abstractly, you can come to understand that the directions that music went aren’t completely arbitrary. Composers are exploring the possibilities that musical space presents them with.”

Tymoczko built on familiar geometrical analogs for music. For example, musical pitch is often imagined as lying on a line with low notes to the left and high notes to the right. Furthermore, as pitches go higher and higher, the notes repeat in different octaves, such that a low C, a middle C, and a high C all sound very similar. Often, the exact octave of a particular note doesn’t matter very much in music. Instead, musicians commonly visualize a “pitch class circle,” which comes from the original line by gluing together each point of the line that represents the same note in different octaves. So low C, middle C, and high C, for example, would all be glued together.

Applying the same kind of reasoning to complete pieces of music, Tymoczko created a geometric space in which he could analyze a piece of music with two notes being played simultaneously. He started with a piece of paper and made the horizontal direction represent the pitch of one note and the vertical direction represent the pitch of the other. A piece of music with two voices would correspond to dots moving around in this space.

Then he modified the space to embed musical structure within it. First, Tymoczko used the same method musicians used to create the pitch circle. He glued the left edge of the page to the right edge, turning the horizontal lines into circles and creating a cylinder from the whole page. Then he glued the bottom end of the cylinder to the top, turning the vertical lines into circles as well and creating a donut shape from the entire page.

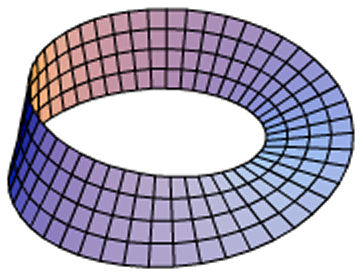
Next, he noted that the order of the notes in a chord doesn’t much matter. That means that the point on his page that has C in the horizontal direction and E in the vertical direction is really the same as the point that has E in the horizontal direction and C in the vertical direction. So he took his space and glued all those points together. It takes a bit of effort to visualize it, but for two simultaneous notes, this turns the donut shape into a Möbius strip.

Tymoczko used the same method to create geometrical spaces to model pieces with any number of simultaneous notes. A piece with three notes, for example, would correspond to points in three-dimensional space. When he wrapped the space around to form circles and identified chords with the same pitches in a different order, he created a twisted prismatic donut. More notes require more than three dimensions, which gets hard to picture but not so hard to describe mathematically.

Having constructed his spaces, he began translating musical principles into their geometric equivalents. He noted that if he plotted a major chord in his geometrical space and reflected it, as if across a mirror down the middle of the space, it turned the chord into a minor one. Rotating a chord to a different spot in the space corresponded to transposing the chord into a different key. Composers need to choose sequences of chords that the ear can make sense of harmonically, and Tymoczko noted that this tends to be accomplished by transitioning between chords using combinations of these geometric rotations and reflections, or approximations to them.

Composers also need to write music in such a way that our minds can link the sounds into simultaneous, overlapping melodies. This is this easiest when each individual melody moves only in fairly small steps.

The trick for composers is to accomplish both those goals, harmonic and melodic consistency, at the same time. “We’ve just translated that into a math problem,” Tymoczko says. “The solution is to use sequences of points close together that are related by rotation, or nearly so.”

Music theorists have long found Chopin’s E minor prelude puzzling. Although the chord progressions sound smooth to the ear, they don’t quite follow the traditional rules of harmony. When Tymoczko looked at the piece and watched the composition’s motion through his geometrical space, he saw that Chopin was moving in a systematic way among the different layers of the four-dimensional cubes. “It’s almost as if he’s an improviser with a set of rules and set of constraints,” Tymoczko says.

What’s particularly amazing, Tymoczko says, is that the mathematics needed to describe these spaces wasn’t even developed in Chopin’s time. Nevertheless, he says, “it is unquestionable that he had some cognitive representation of the space. So there was this period of history where the only way Chopin could express this abstract knowledge was through music. His knowledge of four-dimensional geometry was most efficiently expressed through piano pieces.”

---

If you would like to comment on this article, please see the blog version.