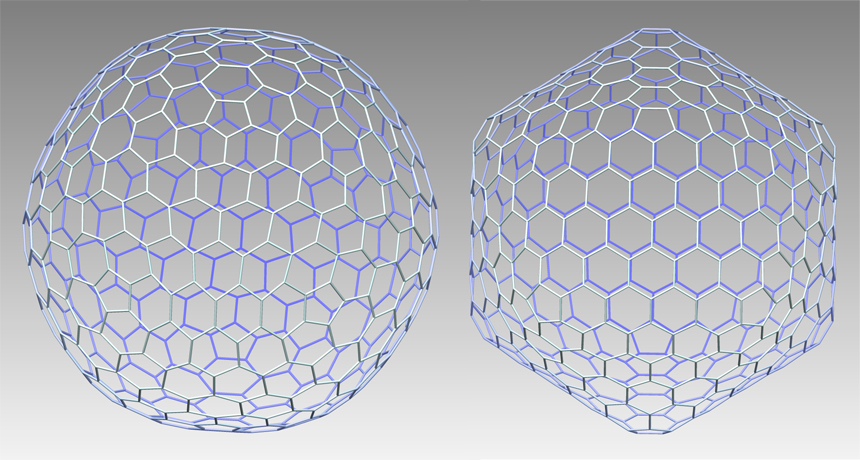
SHAPE SHIFTER A new type of molecular cage has all sides of equal length and flat faces that are all pentagons or hexagons (left). The hexagons have angles that vary from 104 to 142 degrees. A fullerene with the same number of vertices and the same pattern of faces (right) has hexagons with angles that vary in a much narrower range. This forces the hexagonal faces to warp and the cage to assume a pointy shape.
Molecular graphics performed with the University of California, San Francisco Chimera package. Figure provided by S. Schein.
In the latest verse of a centuries-old mathematical refrain, scientists have figured a way to iron out the wrinkles in a large class of molecular cages. The cages have faces consisting of 12 regular pentagons and up to 480 irregular hexagons, which puts them into a well-known category of shapes called fullerenes. However, unlike most previously known fullerenes, the new shapes’ hundreds of faces are flat rather than warped, and the atoms in the molecule are equally spaced.
The shapes’ flat faces make them convex polyhedra, a type of highly symmetric, faceted solid first studied by the ancient Greeks. The first class to be discovered, called the Platonic solids, consists of solids with identical faces that are all regular polygons, meaning shapes with equal sides and angles. There are only five such solids, the most complicated of which is the icosahedron (familiar to game players as the shape of 20-sided dice). A less restrictive class, called the Archimedean solids, allows the faces to have different shapes, though they still must be regular polygons. An even less restrictive class, discovered by Johannes Kepler in 1611, allows quadrilateral faces with equal side lengths but unequal angles.
The new shapes don’t fit into any of these categories. “This is the first new class of convex, equilateral polyhedra with icosahedral symmetry in 400 years,” says UCLA neuroscientist Stan Schein. In Schein’s polyhedra, the hexagonal faces have equal side lengths but unequal angles. Schein’s work, which he performed with UCLA neuroscientist James Gayed, appears February 10 in the Proceedings of the National Academy of Sciences.
Long the province of mathematicians, polyhedra attracted increasing interest in the 20th century from biologists and chemists. In 1962, Aaron Klug and Donald Caspar discovered that certain viruses have an icosahedron shape. In 1985, chemist Richard Smalley andcolleagues discovered that carbon forms cages of 60 or more atoms. They called the 60-atom shape “buckminsterfullerene,” though it was already known to mathematicians as a truncated icosahedron — and to nonscientists as a soccer ball.

Schein came to the cage-shaped molecules because he was curious about clathrin, a protein that assembles itself in cages. Making physical and computer models of these shapes, he was struck that some of them were, he says, “ugly”: If he made the edges equally long, he couldn’t get the faces to lie flat. In fact, all fullerenes other than the 20-atom dodecahedron and the 60-atom soccer ball have this defect. Yet pictures of them tend to fudge these distortions. “A lot of people say that fullerenes are convex polyhedra, but from the point of view of a geometer, the faces of a polyhedron must be planar,” says Schein. In addition, the faces warp in such a way that the solid cannot be convex.
Schein developed a way of measuring warpedness, which he calls the dihedral angle discrepancy. If you open a greeting card so that the bottom edge opens only to an angle of 30 degrees, while the top edge opens to 90 degrees, you will be forced to warp the front of the greeting card. The discrepancy, 60 degrees, measures how much warp is necessary. Schein then experimented with various fullerenes, to see whether the dihedral angle discrepancy could be set to zero.
He was surprised to discover that, for a particular class of fullerenes called Goldberg polyhedra, all of the faces can flatten simultaneously. These solids were discovered in 1937 by mathematician Michael Goldberg . They are the most highly symmetric fullerenes, with all of the rotational symmetries of a soccer ball or an icosahedron.
The Goldberg-type polyhedra that Schein and Gayed found have hexagonal faces with sides of equal lengths but not equal angles, as well as pentagonal faces that retain both equal sides and equal angles. In addition, they retain the 60-fold rotational symmetry of the original Goldberg polyhedra. Using computer software, the team constructed such polyhedra with as many as 980 vertices.
When the number of vertices is large, these polyhedra are hard to tell apart from a sphere. By contrast, conventional fullerenes approach a distinctly nonrounded shape. The roundedness of the Goldberg polyhedra might make them more useful for applications where a spherical shape matters — say, for designing better patterns of dimples on a golf ball. The flat faces could make them a relevant model for molecular cages with double bonds, Schein points out, because such bonds are more resistant to warping than single bonds.
Though Schein’s and Gayed’s fields of study venture far from geometry, mathematicians applaud their finding. “It is correct, and the result is new,” says Branko Grünbaum, a mathematician at the University of Washington in Seattle.
Mathematicians have overlooked the equilateral Goldberg polyhedra, Grünbaum says, because researchers have cared more about the number and pattern of the faces than about concrete questions such as how long the sides are and what the angles between them have to be. Egon Schulte, a geometer at Northeastern University in Boston, agrees. “You have to get your hands dirty to answer those questions,” he says.
That attitude may soon change. Mathematicians may start to look for additional classes of convex polyhedra with equal sides, says Schulte. “It’s not even clear that there are only finitely many classes.” The club that began with Plato and Archimedes may have more members to come.
Editor’s note: This story was updated on February14, 2014, to correct the discipline of James Gayed.






