A Golden Sales Pitch

Can mathematics sell blue jeans? One company is hoping so.

The ProportionofBlu is a Los Angeles–based vendor of blue jeans designed to incorporate the celebrated golden ratio. The golden ratio is approximately 1.618:1, and it’s defined as the ratio a : b such that a/b = (a + b) / a. Many have claimed that the golden ratio has divine, mystical, or highly aesthetic properties.

The company says that the ratio was used to design details such as the curve of the front pocket, the proportions of the rear pocket, and the ratio of the hip stitching to the inseam of the jeans. “This ratio is found throughout nature and has been recognized as a fundamental component of all things that man has found aesthetically pleasing,” says a ProportionofBlu press release.

The blue jeans may be attractive, but the golden ratio probably doesn’t have much to do with that. There is little evidence to suggest that the golden ratio has any special aesthetic appeal.

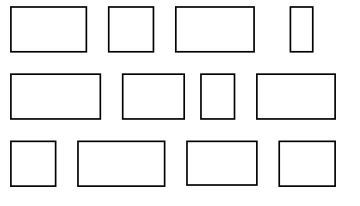
Those who believe that it does usually cite an experiment from the 1860s showing that when asked which rectangle is the “most pleasing,” people most often choose the “golden rectangle” whose sides represent the golden ratio. More recent and rigorous versions of the experiment have debunked that finding. In a 1966 experiment by H.R. Schiffman of Rutgers University, for example, participants said that the most pleasing rectangles were those with a length to width ratio of about 1.9, on average, rather than 1.618. And the relationship between a pleasing rectangle and a pleasing pair of jeans is less than obvious anyway.

The company press release goes on to say, “Recognizing the inherently pleasing nature of things ‘in the ratio,’ man has employed the Golden Ratio throughout time in some of the most remarkable and inspiring achievements. These include the Parthenon in Greece, the ancient Pyramids in Egypt, da Vinci’s Mona Lisa and Stradivarius’ Violins.”

When a myth is repeated over and over, it can begin to sound like the truth.

Most of these examples are inaccurate. The actual ratio of the width to the height of the Greek temple called the Parthenon is about 2.25:1, not 1.618:1. The Great Pyramid of Khufu has proportions nowhere near that of the golden ratio, despite claims to the contrary that seem to be based on a wildly inaccurate 1859 translation of the Greek historian Herodotus. And a golden rectangle drawn over the Mona Lisa does not frame her face.

One of the four examples is accurate, however. Original drawings show that Antonio Stradivari placed the eyes of the f-holes of his violins at positions determined by the golden ratio. However, experts don’t believe that this placement contributes to the high quality of the instruments (See SN: 6/30/07, p. 414).

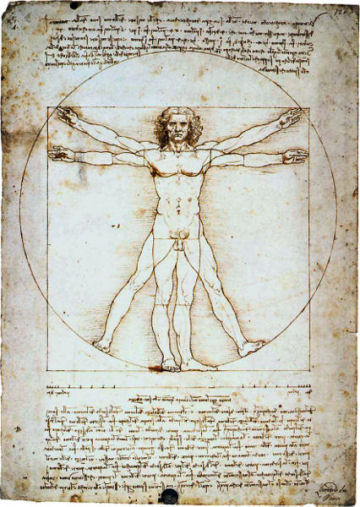
I, too, was fooled by the myths, and to my regret had a hand in further perpetuating them. In the recent MathTrek article, “The Mathematical Lives of Plants”, I repeated the often-stated claims that the ancient Greeks believed that the golden ratio has divine and mystical properties and that Leonardo da Vinci believed that the human form displays the golden ratio. Neither assertion is proven, and I have since corrected the error.

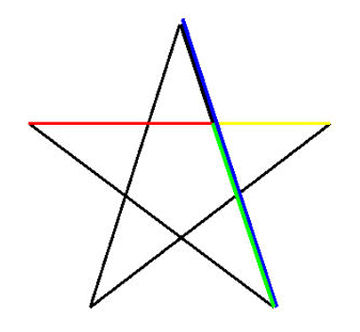
The ancient Greeks studied the golden ratio extensively, but there is no evidence that they considered it to have divine or mystical properties. Euclid’s book, The Elements of Geometry, describes the golden ratio (which he called “division in extreme and mean ratio”) in great detail, but Euclid focused only on its mathematical properties. He was interested in it primarily because the golden ratio is essential for constructing a pentagon using a straightedge and compass. Euclid uses the pentagon to construct the dodecahedron and the icosahedron.

The claims about Leonardo da Vinci seem to stem primarily from his work illustrating The Divine Proportion, a 1509 book by his friend Luca Pacioli which contains the earliest known claims that the golden ratio has divine properties. However, while the book extols the golden ratio and advocates a careful study of proportion in the arts, it recommends that buildings and paintings be planned using a system of simple, rational ratios, not the golden ratio.

Myths about the golden ratio seem to endure largely because the idea of a mathematical object with aesthetic powers is too alluring to resist. Whether it has the power to sell blue jeans has yet to be seen.

Note: In the set of rectangles shown above, the rectangle on the bottom row, second from the right, has proportions closest to the golden ratio.

---

If you would like to comment on this article, please see the blog version.