Mathematical forms are no longer unusual sights at the annual International Snow Sculpture Championships in Breckenridge, Colo. For 7 years, mathematician Stan Wagon of Macalester College in St. Paul, Minn., and his team have carved huge blocks of snow into graceful geometric shapes.

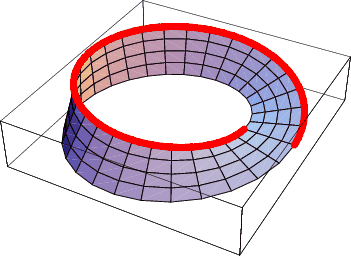



This year, the team took on a particularly challenging, intricately convoluted form—one that incorporated the intriguing surface known as a Möbius strip.
A Möbius strip (or band) is a remarkable surface having only one side and one edge. You can make a model of one by joining the two ends of a long strip of paper after giving one end a 180-degree (or half) twist.
Cutting a Möbius strip down the middle along its length produces not two separate bands but a single, twisted loop that is twice as long as the original loop and has a 360-degree twist.
Intriguingly, you can also get a one-sided, one-edged band by joining the two ends of a long strip of paper after giving one end three half-twists instead of just one. If you were to lay a string along the strip’s edge until the string’s ends met and pulled the string tight, you would end up with a trefoil knot in the string. If you did this with a standard Möbius band, you wouldn’t get a knot.
Splitting a triply twisted Möbius strip down the middle yields a single, twisted loop tied into a trefoil knot.
In general, all bands with an odd number of half-twists (and their mirror images) are, roughly speaking, one-sided surfaces. Bands with no twist or an even number of twists have two sides. Topologists generally apply the term “Möbius band” not only to the standard form (one half-twist) but also to the symmetric version (three half-twists) and anything else “homeomorphic” to the standard form.
For this year’s snow-sculpting competition, computer scientist Carlo H. Séquin of the University of California, Berkeley created an elegant design based on a split, triply twisted Möbius strip (see http://www.cs.berkeley.edu/~sequin/SCULPTS/SnowSculpt05/). He then generated three-dimensional, scale models of the structure to guide the snow carving.
This year’s snow-carving team consisted of Wagon, Séquin, John Sullivan of the Technical University of Berlin, Dan Schwalbe of Minneapolis, and Richard Seeley of Silverthorne, Colo.
The challenge of carving this particular form became apparent early on. A practice block crashed, but the carvers did learn some valuable lessons from the experience. Then, it was time to start on the 10-foot-by-10-foot-by-12-foot snow block made available to the sculptors for the competition.
The snow carvers in the competition had four-and-a-half days to complete their creations. The Minnesota team spent much of the first 2 days removing more than half of the 20 tons of snow in their block to obtain a rough approximation of a triply twisted band. In the remaining time, the team split the structure’s three lobes lengthwise and sculpted the resulting bands into crescent-shaped cross sections.
Amazingly, the fragile structure was still standing for the judging and subsequent public viewing. It didn’t win a prize, but it was still a tribute to the power and beauty of mathematics. Interestingly, the winning entry, from a Tennessee team, also featured a mathematical shape—an intricate rendition of the shell of a nautilus (see http://www.gobreckevents.com/isscsnowsculpture.htm).
Puzzle of the Week
A bag of candy sits on a table. If two kids share all the candy so that each one gets the same number of pieces, there’s one candy left over. If three kids share the same candy equally, there are two candies left over. If four kids share the candy equally, there are three candies left over. If five kids share the candy equally, there are four candies left over. If six kids share the candy equally, there are five candies left over.
How many candies are in the bag?
For the answer, go to http://www.sciencenewsforkids.org/articles/20040317/PuzzleZone.asp.






