In M.C. Escher’s lithograph “Ascending and Descending,” monks are trudging along on a staircase. Some are climbing up and some are walking down, but each monk will end up back at his starting point. The staircase connects to itself, forming a square.
Of course, a real staircase can’t lead to its starting point; Escher’s image is an optical illusion. He learned about the concept in a 1958 article by mathematician Roger Penrose and his father, psychiatrist and mathematician Lionel Penrose.
A very similar illusion is musical rather then visual. In 1964, Roger N. Shepard of Stanford University created an auditory illusion of a musical scale that seems to ascend forever. Psychologist Diana Deutsch of the University of California, San Diego has recently produced an improved version in which the illusion is even stronger. Just as optical illusions have helped psychologists understand how humans process what they see, auditory illusions are shedding light on how our brains process sound.
Audio 1
(Courtesy A.J.M. Houtsma, T.D. Rossing, and W.M. Wagenaars. From “Auditory Demonstrations,” an audio CD distributed by the Acoustical Society of America.)
Audio 2
(Courtesy Diana Deutsch)
The first audio file above is Shepard’s version of an ever-ascending scale. The second is Deutsch’s modification.
Escher and the Penroses created their visual illusion by slightly tweaking the laws of perspective. Our brains create a three-dimensional image from lines on a page based on the angles at which they intersect. By slightly skewing those angles, the image fools us into conjuring up a three-dimensional object that could never exist.
If the lithograph represented an actual three-dimensional object, that object would be different from the one we imagine. The four sets of stairs that form the staircase wouldn’t meet. Instead, one set of stairs would simply drop off into a void. The particular viewpoint of the image makes it look as though the stairs meet in a square even though that is impossible.
The ever-ascending scale takes advantage of peculiarities in how we perceive sound. Sound is made up of waves of varying frequency. In each musical note, one particular frequency is the strongest. The shorter the wavelength, the higher the pitch we hear.
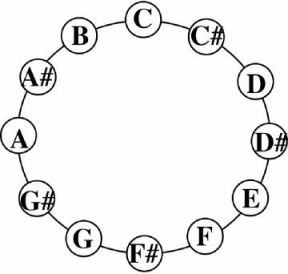
But when the primary frequency of one note is double the primary frequency of another, the two notes sound similar. In Western music, we give both notes the same letter name and use the notion of octaves to distinguish them. Music theorists say that such notes have the same “pitch class.” For example, tones with primary frequency of 220, 440 or 880 Hertz are all heard as the note A.
Altogether, there are 12 pitch classes. They form a circle, with each pitch class separated by a semitone.
For each pitch class, Shepard constructed a tone composed of ten different frequencies of that pitch class, giving the middle frequencies the highest volume. This makes it impossible to determine which octave the tone is in. Shepard played these 12 tones in clockwise succession around the circle of pitches. Because of the octave ambiguity, the sounds seem to rise endlessly while also circling endlessly.
Deutsch has recently created an improved version of the Shepard scale, which uses a more sophisticated method of constructing the composite tone to make the illusion even stronger. Her method can be used with the more complicated waveforms produced by acoustic instruments, rather than relying on electronically generated tones. She will present the method in August at the annual conference of the Society for Music Perception and Cognition in Montreal.
Deutsch has used the illusions to investigate the nature of musical perception, and her results suggest that most people may possess a rudimentary form of perfect pitch.
She exploited a peculiar property of Shepard tones. When two Shepard tones are heard in succession, they seem to rise if the clockwise distance from the first note to the second is less than half an octave (A to C, for example), and they seem to fall if the clockwise distance is greater than half an octave (C to A, for example). But what happens when the two tones are exactly half an octave apart? Listen to this sequence of notes. Which pairs of notes are rising and which are falling? (Audio file courtesy Diana Deutsch)
This produces an astonishing phenomenon. A room full of trained musicians can listen to a series of Shepard tones that are each half an octave apart (called a tritone), and half the people will swear the tones were rising, while the other half will swear they were falling. “They’re stunned,” Deutsch says. “They just can’t believe it.” The reality is that there is no correct answer, since Shepard tones neither rise nor fall.
Deutsch found that people who heard the tritone A to D-sharp as rising did so fairly consistently whenever they heard that particular series of notes, although another person might hear the same series as falling. Furthermore, a person who heard A to D-sharp as rising would hear D-sharp to A as falling.
A few people can name notes upon hearing them in isolation, and they are said to have perfect pitch. Most people recognize only relative pitch, however: they can recognize that the interval of a minor third is the same whether it starts on an A or a D-sharp, for example, but they can’t name any of the notes involved.
When Shepard tones are used, the interval of a tritone sounds different depending on which note it starts on. For example, for some people it seems to rise if it starts on an A and fall if it starts on a D-sharp. This suggests that our brains recognize, to some extent, the pitch class itself and not just the relationship between different notes. Thus, most of us may possess a rudimentary form of perfect pitch.
If you would like to comment on this article, please see the blog version.






