What’s the largest number of pennies that you can pack inside a circular tray to form a carpet of non-overlapping coins? What about inside a square or triangular tray? What if you could expand or contract the size of all your pennies to fit a required number of them snugly in a given tray?



Mathematicians have long pondered the problem of packing identical circles inside a variety of geometric shapes. Indeed, “the optimal packing of equal disks . . . is an ancient and extremely difficult problem,” says mathematician Ronald L. Graham of the University of California, San Diego. “Some of these very simple problems—like how you pack 27 disks in a triangle, square, or circle—are very stubborn.”
There are several different ways to approach disk-packing questions. In one set of problems, you try to pack identical disks inside a larger circle with a fixed radius. Your goal is to place n identical disks within the larger circle in such a way that their common radius, rn, is as large as possible. The corresponding placement is called an optimal packing.
Instead of fixing the radius of the larger circle and searching for the maximum radius of the disks in the packing, you can equivalently search for the minimum ratio of the radius of the larger, enclosing circle to the radius of a disk in the packing without fixing either radius. In this case, you can also try to optimize the density of the packing, which is the area occupied by the disks of the packing divided by the area of the larger, enclosing circle.
The optimal dense packing for two disks in a circle is one in which the disks are in a line and the enclosing circle has a radius equal to the diameter of one of the disks. For three disks, the optimal packing is a triangle of disks; for four disks, a square; and for five disks, a pentagon. For six disks, there are two optimal patterns.
Starting in the 1960s, mathematicians worked out optimal packings for as many as 11 disks enclosed in a circle, and they suggested possible patterns for the cases involving 12 to 20 disks.
Proving that a particular pattern is optimal, however, is no simple matter. For example, it was only in 1994 that Hans Melissen proved optimality for 11 disks.
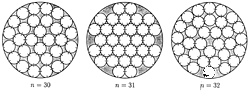
Peculiarities abound. In the 18-disk case, there are 10 different patterns that all share the title of best packing found to date. The disks also fit within a circle of the same radius as that for the best packing identified so far for 19 disks. But no one knows yet whether these patterns represent the optimal arrangements.
Much less is known about 20 or more disks in a circle. To tackle larger numbers of disks, Graham, Boris D. Lubachevsky, and various collaborators have turned to computer-aided methods to construct efficient, tight packings of large numbers of disks.
One technique that has proved effective simulates the idealized movements of billiard balls inside a circular or square table. In his computer model, Lubachevsky starts with a given number of points—tiny disks—randomly spread out over a circular or square area. The disks move around like billiard balls, colliding, rebounding, and changing speed. As the disks roam, their diameters gradually increase, so the disks have less and less space within which to move. Eventually, they get locked into some sort of packing.
By trying the procedure hundreds of times for a given number of disks, started in random positions and at random velocities, it’s possible to zero in on a good packing.
“If the same pattern comes up 700 times, you begin to believe it,” Graham says. In fact, this ingenious approach has now produced many of the best packings anyone has yet found for up to 65 disks in a circle. In a few cases, the packings have been proved optimal.
David W. Boll, a software development engineer in Colorado, got interested in packing circles when he read an article by Martin Gardner in which Gardner discussed the problem of packing 10 identical circles in the smallest possible square.
Independently, Boll developed a computer algorithm for finding good packings for circles in squares, circles in larger circles, and spheres in cubes. Boll and co-worker Jerry Donovan, who developed a somewhat different computer program to do the same thing, now hold a number of records for the best known solutions for packing circles in a square.
In 2000, Boll and Donovan collaborated with Graham and Lubachevsky on a paper describing a new numerical procedure for generating dense packings of disks and spheres inside various geometric shapes.
When applied to previously studied cases of packing n equal disks in a square, the procedure confirmed all the previous record packings, except for n = 32, 37, 48, and 50 disks, where better packings than those previously recorded were identified. Many of these earlier configurations had been found by Kari J. Nurmela and Patric R. J. Östergård.
“For n = 32 and 48, the new packings are minor variations of the previous record packings,” the researchers note. “However, for n = 37 and 50, the new patterns differ substantially.”
There are lots of directions in which disk-packing research can go. Graham, Lubachevsky, and others have already investigated disk packings in squares and equilateral triangles. Lubachevsky and physicist Frank Stillinger have used expanding billiard balls—as many as 10,000 at a time—to model the movements of tiny dislocations in crystals and other aspects of the behavior of materials.
However, there are limits to what anyone can do, even with a powerful computer and a clever algorithm. “Will I live to know the ‘truth’ for . . .1,000 disks in a square?” Graham asks. “Almost certainly not!”
Originally posted: Nov. 23, 1996
Updated: Dec. 11, 2004






