Many of you are probably familiar with the two-player, pencil-and-paper (or electronic) game known as Battleships.
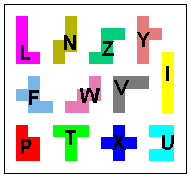



On separate 10-by-10 grids of squares, each player deploys a fleet consisting of one battleship (four consecutive horizontal or vertical squares), two cruisers (three squares each), three destroyers (two squares each), and four submarines (one square each). The two players then take turns “shooting” at each other’s hidden fleet by calling out the coordinates of a square in the grid. The opponent must say whether a shot has missed or hit, and if a hit, what it has hit. Play continues until a player succeeds in sinking the opposing fleet.
The same sort of idea can be applied to other combinations of grids and geometric objects to create various intriguing recreational puzzles.
Mogens Esrom Larsen of the University of Copenhagen has studied a Battleships variant in which the grid is an eight-by-eight checkerboard and the pieces are units called pentominoes.
Whereas a domino is simply two squares stuck together along one edge, a pentomino consists of five adjacent, or “simply connected,” squares. There are 12 different pentominoes.
A standard checkerboard is made up of 64 squares, and the 12 different pentominoes have a total of 60 squares. It’s possible to cover a checkerboard with the 12 pentominoes, leaving four unoccupied squares. In fact, there are lots of different ways to do so, leaving the four empty squares as one block somewhere in the grid or as four separate squares.
Here’s an example of how the 12 different pentominoes can cover a checkerboard, leaving four unoccupied squares. |
The goal of pentomino battleships is to locate the four unoccupied squares of an opponent’s hidden grid. Each player, in turn, shoots a volley of four shots aimed at hitting the empty squares. The opponent states how many shots hit which pentomino.
How would you start?
In the example above, a player has fired shots at a1, b1, a8, and h8. The opponent replies that the volley hit the N pentomino twice, the Z pentomino once, and the P pentomino once. This information locates the N, but it could be in either one of two possible orientations. The other two pentominoes are in the corners.
Given this information, where would you fire the next volley? Suppose you shoot at b2, h2, h7, and h8. In this case, you find out you have hit the I twice, the L, and the Z. That’s enough information to place the N, the I, and the Z. But the P still has six possible orientations, and the L has five different possible orientations.
How many more volleys do you think you would need to locate the four empty squares? Is there an optimal firing strategy?
The general answer to these questions depends on the arrangement of the pentominoes on the hidden grid. It’s very likely that some arrangements would be easier to solve than others.
You could, for example, try to take advantage of the F pentomino’s asymmetry. Placed in a three-by-three square, the F by itself gives four empty squares, and there are eight different ways to place those vacancies.
The strategy then would be to come up with an arrangement of 12 pentominoes that not only incorporates this three-by-three configuration but also places it as far away as possible from a corner of the checkerboard. Even if an opponent hits the F, he or she would still need several subsequent shots to locate all four empty squares.
Puzzle: Is there an arrangement of pentominoes that accommodates such a central or nearly central F square?
That’s just one of the puzzles suggested by pentomino battleships. It’s an interesting realm ripe for further exploration.






