A magic cube is a three-dimensional array of whole numbers, in which each row, column, and body diagonal (corner to corner, through the center) adds up to the same total. A perfect magic cube is one in which the diagonals of each vertical or horizontal slice through the cube also sum to the same value.
Suppose each row, column, and diagonal contains N numbers. The magic cube would then consist of N3 numbers, usually the integers from 1 to N3. In this case, the sum (or magic constant) is 1/2(N4 + N).
So, for N = 5, there would be 125 numbers in the array and the sum of each row, column, and diagonal would be 315. The number N is called the order of a magic cube.
There are no perfect magic cubes of order 2, order 3, or order 4.
For a long time, no one was sure whether there existed a perfect magic cube of order 5.
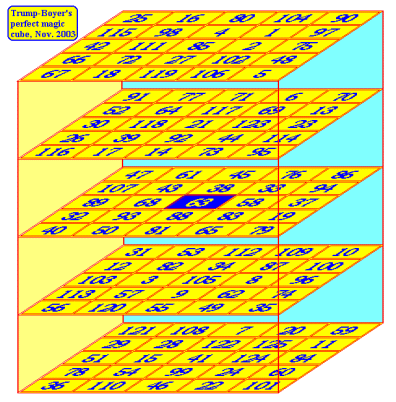
In 1972, Richard Schroeppel proved that, if a perfect magic square of order 5 exists, its center number must be 63.
Last November, Walter Trump and Christian Boyer finally found a perfect magic cube of order 5.
The first known perfect magic cube of order 5. |
As expected, the cube’s magic constant is 315, and its central value is 63. Moreover, there are 109 ways to get the magic sum: 25 rows, 25 columns, 25 pillars, 4 body diagonals, and 30 face diagonals.
Boyer and Trump ran five computers for several weeks to come up with their solution, checking a large number of “auxiliary” cubes of order 3 to find the right combination.
Interestingly, just 2 months earlier, Trump had found the first perfect cube of order 6.
These recent discoveries leave the existence of perfect magic cubes of order 10 as the next unresolved question.






