- More than 2 years ago
In the realm of mathematics, it’s hard to imagine anything more basic than the counting numbers: 1, 2, 3, and so on. Yet this set of mathematical objects abounds with beautiful and unexpected patterns. For example, pick any number and double it. You’ll always find a prime number—a number divisible only by itself and by 1—between that number and its double. As another case in point, primes that leave a remainder of 1 when divided by 4 can always be expressed as the sum of two squares. Now, a mathematics graduate student has put what may be the final piece into the picture of one of the most surprising patterns of all.
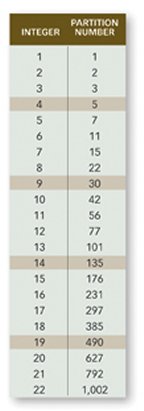
Working despite his adviser’s warnings that the problem was exceedingly difficult, Karl Mahlburg of the University of Wisconsin–Madison has come up with an explanation for a particular infinite collection of patterns. They concern partitions—ways of breaking up a number into a sum. The number 4, for instance, has five partitions (see illustration, below). The number 5 has 7 partitions, and the number 6 has 11 partitions. The partition numbers quickly skyrocket: For instance, the partition number for 50 is 204,226 and for 200, it’s 3,972,999,029,388.
To number theorists, partitions are among the most tantalizing objects in mathematics. However, even the simplest questions about the properties of partitions can be very hard to answer. For instance, no one has proved whether there are infinitely many partition numbers divisible by 3, although it’s known that there are infinitely many partition numbers divisible by 2. There isn’t much to distinguish a difficult question from one that can be easily solved, says Ken Ono, Mahlburg’s adviser at Wisconsin.
While partitions were originally studied for their intrinsic interest, they have turned out to underlie a wide swath of mathematics, including some of the ideas that went into the proof of Fermat’s last theorem by Andrew Wiles in 1993. Partitions also play a role in physics. For example, theoretical physicists employ them to explore the ways in which a collection of particles can be distributed among different energy configurations.
Surprising patterns
Fundamentally, partitions describe how to put together a number via addition. Yet, in 1919, Indian mathematician Srinivasa Ramanujan discovered that partitions have an unexpected connection to multiplication. They show patterns that rely on prime numbers, the building blocks for putting together a number via multiplication.
Ramanujan found that starting with the fourth partition number, which is 5, every fifth partition number is divisible by 5. For instance, the number 4 has 5 partitions, 9 has 30 partitions, and 14 has 135 partitions (see illustration, above).
Ramanujan also discovered that starting with the 5th partition number, every 7th partition number is divisible by 7, and starting with the 6th partition number, every 11th partition number is divisible by 11. These three patterns are called Ramanujan’s partition congruences.
“These patterns are very unexpected,” Ono says. “There’s nothing about the definition of partitions that gives an easy explanation for why the three Ramanujan congruences exist.” These congruences forge a link between two ways of expressing numbers—as sums and as products.
The numbers 5, 7, and 11 are consecutive primes, and the next prime is 13. So, extrapolating from Ramanujan’s patterns, it makes sense to predict that, starting with the 7th partition number, every 13th partition number should be divisible by 13. Yet this is not so. After the three Ramanujan congruences, the pattern mysteriously breaks down.
For decades, mathematicians supposed that Ramanujan’s three patterns were the only ones. In 1968, however, A. Oliver L. Atkin of the University of Illinois at Chicago discovered a few additional, much more complicated congruences. For instance, starting with the 237th partition number, every 17,303rd partition number is divisible by 13.
Then, in 2000, Ono astonished mathematicians by proving that partition congruences exist for every prime number, starting with 5 (SN: 6/17/00, p. 396: The Power of Partitions). This result was later generalized by Ono and Scott Ahlgren, now at the University of Illinois at Urbana-Champaign, to include all powers of primes. So, there are congruences not just for 5 but also for 52, 53, and so on.
Although Ramanujan proved that each member of a certain collection of partition numbers is divisible by 5, for example, his proof didn’t give a way to break the number into five equal groups, or into groups of numbers all divisible by 5. In math, such a tangible breakdown is called a combinatorial proof. Ramanujan’s work, and Ono’s after it, relied on more-abstract proofs of divisibility.
Now, Mahlburg has come up with a combinatorial explanation for the unexpected divisibility patterns. His work completes a chain of ideas that was begun 6 decades ago by physicist Freeman Dyson of the Institute for Advanced Study in Princeton, N.J.
Mahlburg’s work finally “gives a natural explanation for these congruences, which explains why they exist,” Ono says.
According to rank
Ramanujan’s three partition congruences caught Dyson’s eye in 1941, when he was at the University of Cambridge in England. He noticed what looked like a way to visualize the divisibility properties of Ramanujan’s first two congruences.
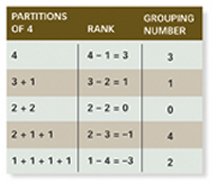
Dyson defined the rank of a partition to be its largest term minus the number of terms in the partition. Take the example of the partitions of 4. One of the five partitions is 3 + 1. Its rank would be 3 – 2 = 1. Rank gives a way to split all the partitions of a number into groups, just as a collection of people can be divided into groups according to, say, height.
To group the partitions of 4, mathematicians divide the rank by 5, and the remainder is the grouping number. They use modular, or clock, arithmetic, to replace each negative number with the positive number with which it would share a position on the face of a clock having, in this case, five numbers. So, before being divided by 5, the rank –1 is replaced by 4 and the rank –3 is replaced by 2.
After looking at many examples, Dyson made a conjecture—proved in the 1950s by Atkin and Peter Swinnerton-Dyer of Cambridge—that in Ramanujan’s congruences for 5 and 7, the rank divides the partitions into five and seven equal-size groups, respectively. In other words, the grouping created by the rank explains concretely why the partition numbers are divisible by 5 or 7.
Oddly enough, the rank doesn’t work to prove Ramanujan’s congruence for 11. It can be used to divide these partitions into 11 groups, but the groups are not equal in size. Dyson conjectured that there must be some other measure of partitions, similar to rank, which does the job for 11. He named this hypothetical measure “the crank.”
For decades, Dyson’s crank was just a name. Then, in 1976, George Andrews, a number theorist at Pennsylvania State University in State College, made an unexpected discovery. At Cambridge University in England, in a box of papers left by the late G.N. Watson, a Ramanujan expert, Andrews came upon a 138-page manuscript handwritten by Ramanujan that contained more than 600 mathematical formulas. Eagerly riffling through the pages, Andrews realized that he was holding the notebook in which Ramanujan had written his final mathematical ideas in the last months of his life, more than half-a-century ago.
“It came as a bolt from the blue,” Andrews says.
Andrews subsequently showed his graduate student Frank Garvan a notebook page. Garvan, now at the University of Florida in Gainesville, saw that one of Ramanujan’s formulas about partitions contained the ingredients that arise in defining Dyson’s rank and proving that it works for 5 and 7. Together, Andrews and Garvan figured out how to modify another of the equations in the notebook to create the crank.
There’s no indication, Andrews says, that Ramanujan realized that his equations could be used for such a purpose.
Andrews and Garvan’s crank is a more complicated expression than the rank, relying on, among other things, the number of 1s in a given partition. Because any partition of a number can be turned into a partition of the next number by adding 1, counting the number of 1s in a partition measures its ancestry, in a sense.
In 1988, Andrews and Garvan showed that the crank could be used to give combinatorial proofs in the same way as the rank can, but this time for all three of Ramanujan’s congruences.
Hidden treasures
Ramanujan’s notebook had not yet yielded all its treasures. In the late 1990s, Bruce Berndt, a number theorist at the University of Illinois at Urbana-Champaign, asked Ono to help him edit for publication a section of the notebook about partitions. On looking at the manuscript, Ono spotted some expressions that he himself had been studying in a context that had nothing to do with partitions. Ono realized that he could use his previous work to prove that partition congruences exist for every prime number starting with 5.
“I was shocked,” Ono recalls.
Ono’s congruence patterns deal with breathtakingly large numbers. For instance, one pattern starts with the 111,247th partition number, which is divisible by 13. To get the next partition number divisible by 13, just add 157,525,693.
It’s not surprising, Mahlburg says, that Ramanujan missed these humongous congruences, since Ono’s work used heavy-duty, number-theory tools not known in Ramanujan’s time.
“The first three congruences are simple enough that Ramanujan could observe them using the naked eye, whereas with Ono’s congruences, the numbers are so large that Ono had to use a telescope to see them, so to speak,” Mahlburg says.
As with Ramanujan’s proof of the first three congruences, Ono’s proof was abstract and so shed little light on just why the partition numbers have these divisibility properties. Could the crank be used to give a concrete explanation for this suddenly expanded universe of partition congruences?
Ono suspected that the answer was yes, but he couldn’t see how to prove it. Then, Mahlburg told Ono that he wanted to tackle the question.
“I warned him that it would take a Herculean effort and there was no guarantee of success, but I didn’t discourage him because he had already written enough papers to qualify for a Ph.D.,” Ono says. “He had the option of either graduating very quickly or trying to hit a home run. He chose the latter.”
Despite Ono’s warnings, Mahlburg says, he had little conception of what he was getting into—which turned out to be a good thing. “If I had known when I started about all the difficulties and dead ends and problems I would have to patch up, it might have been a little too intimidating,” he says. “Fortunately, at each step, there was a small goal toward which I could work, and it wasn’t until I reached that goal that I would realize how far off the next goal was.”
After nearly a year and a half, Mahlburg has succeeded in using the crank to give a concrete explanation for the congruences in the partition numbers.
“It is outstanding work,” Andrews says.
Surprisingly, the crank works differently for the congruences that Mahlburg studied than for Ramanujan’s original three congruences. For Ramanujan’s congruences, Andrews and Garvan proved divisibility by showing that the crank divides the partitions into 5, 7, or 11 equal-size groups. But for the congruences involving larger primes, the groups created by the crank are not equal in size. Instead, each group individually is divisible by the appropriate prime number.
“It’s completely unexpected that the crank should do this,” Dyson says. “It’s independent of the property of the crank that I had conjectured.”
Mahlburg likens his approach to an analogous one for deciding whether a dance party has an even or odd number of attendees. Instead of counting all the participants, a quicker method is to see whether everyone has a partner—in effect making groups that are divisible by 2.
In Mahlburg’s work, the partition numbers play the role of the dance participants, and the crank splits them not into couples but into groups of a size divisible by the prime number in question. The total number of partitions is, therefore, also divisible by that prime.
Mahlburg’s work “has effectively written the final chapter on Ramanujan congruences,” Ono says.
“Each step in the story is a work of art,” Dyson says, “and the story as a whole is a sequence of episodes of rare beauty, a drama built out of nothing but numbers and imagination.”






