What do the following numbers have in common?
3, 7, 31, 127, 8191, 131071, 524287, 2147483647, 2305843009213693951, 618970019642690137449562111, 162259276829213363391578010288127, 170141183460469231731687303715884105727.
Each one is a prime number, evenly divisible only by itself and 1. Each one can also be written in the form a power of 2, less 1: 2p – 1, where p is itself a prime number.
In 1644, French monk and mathematician Marin Mersenne (1588–1648) stated that numbers of the form 2p – 1 are primes only when p has the following and no other values:
p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, and 257.
Mersenne himself didn’t actually test his assertion for any values greater than p = 19. In fact, it wasn’t until 1750 that Leonhard Euler (1707–1783) verified that 231 – 1 (or 2147483647) is a prime.
In 1811, in his book An Elementary Investigation of the Theory of Numbers, Peter Barlow (1776–1862) stated that this prime number “is the greatest that will ever be discovered, for, as they are merely curious without being useful, it is not likely that any person will attempt to find one beyond it.”
It turns out that Mersenne and Barlow were both wrong. In 1903, mathematician Frank Nelson Cole (1861–1926) demonstrated that 267 – 1 is not a prime but the product of 193707721 and 761838257287. At the same time, the discovery of ever-larger Mersenne primes, as these numbers came to be called, steadily progressed to larger and larger values.
Last month saw the discovery of the 42nd known Mersenne prime, the largest prime yet identified. The new Mersenne prime is 225,964,951 – 1. When written out in full, it runs to a whopping 7,816,230 decimal digits. The previous record holder, discovered less than a year ago, consisted of 7,235,733 decimal digits.
The new champion was found by Martin Nowak, a German eye surgeon and participant in the Great Internet Mersenne Prime Search (GIMPS). He used one of his business computers and software provided by George Woltman and Scott Kurowski to find the enormous prime.
Nowak’s computer is one of more than 250,000 computers worldwide engaged in testing Mersenne numbers for primality. GIMPS volunteers are responsible for checking Mersenne numbers within specified ranges of exponents, whenever their computers would otherwise be idle.
In the 10 years since George Woltman started the GIMPS effort, participants have discovered eight Mersenne primes. Nowak, who’s from Michelfeld, Germany, got involved about 6 years ago after he read about GIMPS in his local newspaper. He now has 24 computers taking part in the search.
GIMPS volunteers haven’t yet tested every Mersenne number smaller than the current champion, so another Mersenne prime may yet lurk among the untested numbers. Only exponents less than 15,130,000 have all been tested at least once.
There’s still time to join the search. Maybe your computer will ring up the next champion!
Puzzle of the Week
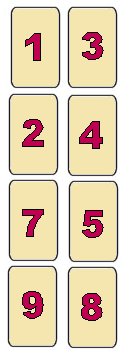
Eight cards are marked with numbers, and the cards are placed in two columns (as shown above). The numbers in the left and right columns add up to different totals.
Rearrange the cards, using as few moves as possible, so that each of the two columns gives the same total.
Courtesy of ThinkFun’s PuzzlePlayground (see http://www.puzzles.com/PuzzlePlayground/WelcomeToPuzzlePlayground.htm).
For the answer, go to http://www.sciencenewsforkids.org/articles/20050105/PuzzleZone.asp.






