Precisely defined yet enticingly elusive, prime numbers occupy a central place in number theory. Evenly divisible only by themselves and 1, these special integers–2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, and so on–pose all sorts of conundrums.

There is no known formula for primes–no combination of algebraic operations on n that will generate, with a few turns of the mathematical crank, the nth prime. To find the 99th prime, all you can do is make an ordered list of prime numbers and count to the 99th.
Nonetheless, there are tantalizing traces of patterns among the primes–and immense frustration attending efforts to elucidate these hints of order. Leonhard Euler (1707–1783) once remarked, “Mathematicians have tried in vain to this day to discover some order in the sequence of prime numbers, and we have reason to believe that it is a mystery into which the mind will never penetrate.”
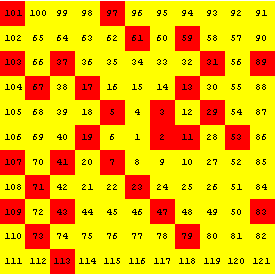
There have been many studies of the distribution of prime numbers and a variety of efforts to visualize this distribution. One particularly intriguing approach is to arrange the integers in a square spiral, starting with 1 at the center of a grid of squares, then mark the squares containing primes. In the following example, the integers go in a counterclockwise spiral.
|
Mathematician Stanislaw M. Ulam (1909–1984) was the first to study such an array. In 1963, while drowsing through a boring talk at a scientific meeting, Ulam had found himself doodling a grid of horizontal and vertical lines. He decided to number the intersections, following a square spiral pattern, then started circling all the primes.
To Ulam’s surprise, the primes tended to crowd into straight lines. They appeared “to exhibit a strongly nonrandom appearance,” he remarked.
When Ulam returned to his job at the Los Alamos Scientific Laboratory, he wanted to see more of the pattern. Taking advantage of a magnetic tape recording the first 90 million primes, he and coworkers Myron L. Stein and Mark B. Wells programmed the lab’s Maniac II computer to display the primes as spots of light on an oscilloscope tube connected to the computer. They then photographed the display to show the primes on a spiral of consecutive integers up to about 65,000.
The patterns were striking. Even at the fringes of the larger grid, the primes tended to pack into not only diagonal but also horizontal and vertical lines.
“It is a property of the visual brain which allows one to discover such lines at once and also notice many other peculiarities of distribution of points in two dimensions,” Ulam and his coworkers remarked in a 1964 paper published in the American Mathematical Monthly.
These lines hint at formulas for primes. Indeed, they can be described by quadratic expressions beginning with 4x2. For example, one diagonal sequence includes the primes 5, 19, 41, and 71. The line along which these primes fall is given by the expression 4x2 + 10x + 5. Giving x values from 0 to 3 generates the four primes. Similarly, the sequence of primes along another diagonal–7, 23, 47, 79–matches the quadratic 4x2 + 4x – 1 (x takes on values from 1 to 4). It’s possible to develop such a formula for just about any line in the diagram.
If you start spirals with numbers other than 1, you find additional lines represented by quadratic expressions. For example, starting with 17 in the central square produces an array in which one diagonal has the formula 4x2 + 2x + 17. One remarkable sequence of primes along this diagonal can also be described by the expression x2 + x + 17, originally discovered by Euler. It generates primes for all values of x from 0 through 15.
Euler’s most famous prime generator is x2 + x + 41. Starting a spiral at 41 produces a grid with an amazing, unbroken sequence of 40 primes along one diagonal. Interestingly, of the first 2,398 numbers generated by the formula, precisely half are primes. Checking all such numbers less than 10 million, Ulam and his coworkers found the proportion of primes to be 0.475.
The researchers also identified several other formulas that are rich in primes. For numbers of the form 4x2 + 170x + 1847, the proportion of primes is 0.466; for 4x2 + 4x + 59, the ratio is 0.437.
Other quadratic expressions rarely give primes. For example, the expression 2x2 + 4x + 117 yields a prime only 5 percent of the time.
Ulam suggested a number of questions worth investigating further. Are there grid lines containing infinitely many primes? What is the maximum prime density of a line? Is the distribution of primes the same in every quadrant of the grid?
What happens with other algorithms for numbering the squares? On hexagonal and other types of grids?
A variety of Web pages offer ways to visualize Ulam’s prime spirals. Several point to novel variants in the numbering schemes and in ways of coloring the squares to highlight different types of integers.
In one striking example, by Jean-Franois Colonna, integers are shown as spheres on a square grid, where the radius and color of the sphere is related to the square root of the number of divisors (primes are white and have the smallest radius). For other colorful ideas, take a look at Adrian J.F. Leatherland’s “Pulchritudinous Primes” Web pages.
There is truly not only mystery but also beauty in the distribution of primes.






