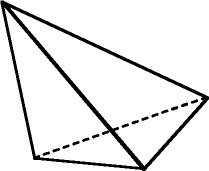

A tetrahedron has four triangular faces, four vertices, and six edges.
Consider what happens when a vertex of one tetrahedron pierces the face of a second tetrahedron to form a new, more complicated polyhedron. In the resulting geometric form, one triangular face has a triangular “hole” where the face was pierced. Mathematicians describe such a punctured face as being “multiply connected.”
Several years ago, mathematician John H. Conway of Princeton University wondered whether a polyhedron could have such a polygonal hole passing through each and every face and remain a polyhedron. He coined the term “holyhedron” to describe this form, should it exist.
Here’s the mathematical question that Conway posed: Is there a polyhedron in Euclidean three-dimensional space that has only finitely many plane faces, each of which is a closed connected subset of the appropriate plane whose relative interior in that plane is multiply connected?
Conway’s specifications exclude polyhedra in which a hole’s sides extend all the way to a pierced face’s edges.
They also explicitly exclude such structures as an infinite lattice of interpenetrating tetrahedra, where each face of each tetrahedron is pierced by the vertex of another.
For a long time, no one could come up with an example, even in principle, that met Conway’s precise specifications for what he meant by a holyhedron. Conversely, no one could say why it was impossible to construct one.
It was, however, possible to come up with structures that met less stringent requirements. Artist and independent scholar George W. Hart created a number of such examples, which looked like holyhedra but failed to meet all of the mathematical criteria specified by Conway (see http://www.georgehart.com/virtual-polyhedra/holyhedra.html).
When Jade P. Vinson first heard about the holyhedron problem, he had just arrived in Princeton as a graduate student. “The problem intrigued me, and the timing was perfect,” Vinson says. “Since the problem required no special background, I could get started right away; and since I hadn’t started on anything else yet, it received my undivided attention.”
That effort paid off handsomely. Vinson’s surprising solution is now slated for publication in the journal Discrete and Computational Geometry.
To solve the problem, Vinson opted to use polyhedra that have more vertices than faces. “The first key idea. . .was to find a simple, repetitive arrangement of polyhedra so that there is a large excess of unused vertices over unpierced faces,” Vinson says. “The second key idea was to ‘trade’ several unused vertices in an inconvenient location for a single new vertex in a better location.”
Given these two ideas, “it is possible to construct a holyhedron with a very large number of sides,” he remarks.
Vinson’s careful manipulations produced a monstrous holyhedron with 78,585,627 faces. “The current construction is hard to visualize,” Vinson admits. Simple cardboard models give just the roughest idea of how it all fits together.
Conway had offered a reward of $10,000–divided by the number of faces–for finding a holyhedron, so Vinson’s initial effort netted him a minuscule return. Conway suspects that someone may yet find a holyhedron with far fewer faces–perhaps only 100 or so.
It would be even nicer, Vinson says, if the discoverer could also construct a convincing cardboard model of this three-dimensional structure.






