


Born in Hartford, Conn., in 1928, artist Sol LeWitt has often featured geometric and combinatorial themes in his numerous creations. His frequent use of simple grids and modular structures and his choice of a palette of just primary colors plus black and white reflect a strongly back-to-basics approach to design.
“I will refer to the kind of art in which I am involved as conceptual art,” LeWitt once wrote. “In conceptual art the idea or concept is the most important aspect of the work. When an artist uses a conceptual form of art, it means that all of the planning and decisions are made beforehand and the execution is a perfunctory affair.”
“The idea becomes a machine that makes the art,” he insisted.
That approach is evident in many of LeWitt’s sculptures, paintings, and drawings. His “Four-Sided Pyramid,” installed in 1997 at the National Gallery of Art in Washington, D.C., consists of concrete blocks precisely stacked to form a stark, eye-catching pyramid. In bright sunlight, the blocks and shadows play curious visual tricks on the eye as you view the structure from different angles.
LeWitt’s large-scale wall drawings, painted directly on walls, represent the logical outcome of his desire to create artworks that are as two-dimensional as possible. In the case of “Wall Drawing No. 623” at the National Gallery of Canada, LeWitt came up with the concept for the painting (a double asymmetrical pyramid configuration), specified the colors, and let a team of assistants make the artwork to his detailed specifications.
Many of LeWitt’s earlier artworks were explicitly combinatorial. In 1973, for example, he composed “Straight Lines in Four Directions and All Their Possible Combinations.” This study consisted of a grid of 15 squares, each inscribed with one or more horizontal, vertical, and diagonal lines in different orientations.
When Barry Cipra, a mathematician and writer in Northfield, Minn., first saw this set of drawings, he was intrigued by how the eye automatically tried to connect the lines from one square to the next. In LeWitt’s arrangement, however, none of the horizontal or vertical lines went completely from one side of the grid to the other.
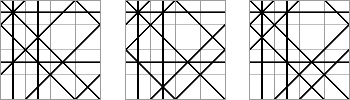
Cipra asked himself if it would be possible to rearrange 16 squares (one of them blank), without rotating any of the squares, so that all horizontal, vertical, or diagonal lines are unbroken within a 4 x 4 grid. That was the birth of a challenging mathematical puzzle.
Playing with square pieces cut from stiff cardboard, Cipra quickly discovered that the puzzle has a solution. John H. Conway of Princeton University then demonstrated that there are actually three solutions.
Rotating any one of the three distinct solutions through 90 degrees, reflecting it, or performing a combination of these two operations generates another, related solution. So does taking the topmost row (or the leftmost column) and moving it all the way to the bottom (or to the right). “In other words, each solution could be drawn on the surface of a torus,” Cipra notes.
Conway and Cipra went on to prove that there are no other possibilities by showing that all solutions must have the toroidal property.
Cipra’s LeWitt puzzle resembles the famous “15” sliding-movement game. A square open tray holds 15 tiles, with one vacant space. The player slides the pieces around in such a way as to rearrange the initial configuration into the desired one. Using such moves, is it possible to go from an arbitrary arrangement of LeWitt’s squares to each of Cipra’s solutions?
Cipra hasn’t tried that yet. However, “it should be straightforward to check whether the three solutions are related by an even or odd number of pairwise interchanges and also how they relate to the initial configuration,” he remarks.
At the same time, Cipra adds, “the LeWitt puzzle is hard enough to solve when you have complete freedom to move the pieces.”
Cipra’s puzzle also serves as a reminder of the essential playfulness and simplicity of LeWitt’s art, where logic, clarity, and beauty interact to evoke visual delight and deep thought.
ANSWER: The three distinct solutions to Barry Cipra’s “Sol LeWitt” tiling puzzle. For the complete explanation, see the link at http://www.akpeters.com/product.asp?ProdCode=1225.






