- More than 2 years ago
The familiar arrangement evident in piles of neatly stacked oranges at a supermarket represents the tightest possible packing of identical spheres (SN: 8/15/98, p. 103: http://www.sciencenews.org/sn_arc98/8_15_98/fob7.htm). The ordered spheres occupy 74 percent of the total space available. The fraction of space typically filled by randomly packed spheres—whether peas poured into a bag or ball bearings into a tin—has proved much more difficult to pin down.
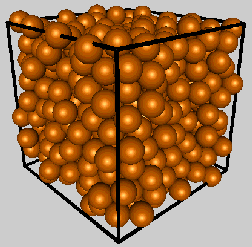
Now, chemist Salvatore Torquato and his coworkers at Princeton University argue that traditional, empirical methods of achieving random packings—pouring followed by shaking for a sufficiently long time, for example—fail to give consistent results. The pouring rate and the amplitude and frequency of vibration can readily affect the final answer, they contend. Computer simulations of random packings reveal similar problems.
To make the notion of random packing more consistent and mathematically precise, Torquato and his colleagues have introduced the concept of what they call a “maximally random jammed” state. A given sphere is jammed if it can’t move when all the other spheres are fixed. The researchers focus on the most disordered arrangement in which all spheres are immobilized. The packing fraction for this state is about 64 percent.
The researchers report their findings in the March 6 Physical Review Letters.






