A square wheel may be the ultimate flat tire. There’s no way it can roll over a flat, smooth road without a sequence of jarring bumps.




Stan Wagon, a mathematician at Macalester College in St. Paul, Minn., has a bicycle with square wheels. It’s a weird contraption, but he can ride it perfectly smoothly. His secret is the shape of the road over which the wheels roll.
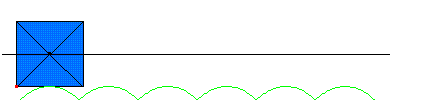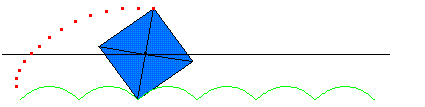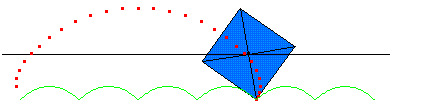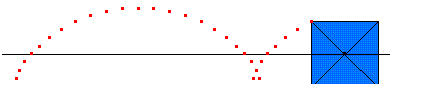
A square wheel can roll smoothly, keeping the axle moving in a straight line and at a constant velocity, if it travels over evenly spaced bumps of just the right shape. This special shape is called an inverted catenary.
A catenary is the curve describing a rope or chain hanging loosely between two supports. At first glance, it looks like a parabola. In fact, it corresponds to the graph of a function called the hyperbolic cosine. Turning the curve upside down gives you an inverted catenary—just like each bump of Wagon’s road.
The Exploratorium in San Francisco exhibits a model of such a roadbed and a pair of square wheels joined by an axle to travel over it (see http://www.exploratorium.edu/xref/exhibits/square_wheel.html).
When Wagon first saw the Exploratorium model a number of years ago, he was intrigued. The exhibit inspired him to investigate the relationship between the shapes of wheels and the roads over which they roll smoothly.
These studies also led Wagon to build a full-size bicycle with square wheels. “As soon as I learned it could be done, I had to do it,” Wagon says.
The resulting bicycle (actually a trike) went on display at the Macalester science center, where it could be seen and ridden by the public. Now, the science center has a new, improved square-wheeled trike. “The old one was falling apart,” Wagon says. “The new one’s ride is much, much smoother.”
Steering remains difficult, however. If you turn the square wheels too much, they get out of sync with the inverted catenaries.
It turns out that for just about every shape of wheel there’s an appropriate road to produce a smooth ride, and vice versa.
Just as a square rides smoothly across a roadbed of linked inverted catenaries, other regular polygons, including pentagons and hexagons, also ride smoothly over curves made up of appropriately selected pieces of inverted catenaries. As the number of a polygon’s sides increases, these catenary segments get shorter and flatter. Ultimately, for an infinite number of sides (in effect, a circle), the curve becomes a straight, horizontal line.
Interestingly, triangular wheels don’t work. As an equilateral triangle rolls over one catenary, it ends up bumping into the next catenary
However, you can find roads for wheels shaped like ellipses, cardioids, rosettes, teardrops, and many other geometric forms.
You can also start with a road profile and find the shape that rolls smoothly across it. A sawtooth road, for instance, requires a wheel pasted together from pieces of an equiangular spiral.
There’s certainly more than one way to ride a bike!
Originally posted: 7/11/98
Updated: 4/3/04






