Sensor Sensibility

Imagine a future in which billions of tiny computers are embedded into buildings, streets, fields, or even our bodies. These devices might monitor weather, traffic, crop conditions, the progression of diseases, or a host of other variables. The tiny computerized sensors would spontaneously organize into networks that could adjust their structures and functions in response to the information that they pick up.

That future might be just around the corner. Researchers have already deployed networks with dozens of matchbox-size sensors in a wide range of applications. Sensor networks are tracking the movement of zebras in Kenya and determining bullet trajectories in military field tests. Coming soon, many engineers predict, are cheap sensors the size of dust particles. Those high-tech specks will measure temperature, vibration, noise, light, and more. The question, the engineers say, is not whether these smart-dust sensors will someday pervade our environment, but when.

For smart dust to be useful, however, engineers must figure out how to build a global view from the information provided by millions or billions of individual sensors.

For example, suppose that agricultural researchers scatter a million battery-powered, smart-dust sensors by helicopter to monitor water levels across a cornfield. Without knowing where each sensor has landed, how would the researchers determine whether the sensors’ combined range leaves gaps? Or imagine that engineers have deployed a sensor network to keep track of boats in a harbor. If each sensor reports how many boats it detects, how can the engineers keep an accurate tally without knowing how many sensors have counted the same boat?

To tackle these questions and others, researchers are drawing on techniques from topology, the study of shapes. Analyzed by mathematicians for more than a century, topology has until recently had few real-world applications.

Yet topology, which pieces together the global structure of a space from local snapshots, is exactly what sensor-network engineers need, argues Robert Ghrist, a mathematician at the University of Illinois at Urbana-Champaign.

“Topology is good for finding hidden features inside a space that you can’t see very well, that you don’t have all the information about,” Ghrist says. “Figuring out the structure of wireless sensor networks is the kind of problem topology was meant to solve.”

Simplex complexity

Unlike geometry, topology focuses on qualitative features—those that don’t change when a shape is stretched and its geometry distorted. This viewpoint may sometimes seem fanciful: For example, to a topologist, a doughnut and a coffee cup represent the same shape since each has one hole. Nevertheless, topologists have developed a powerful arsenal of numerical and algebraic tools that enable them to extract important features from a shape whose precise geometry is unknown.

One of the most famous of such tools is the Euler characteristic, which in its simplest version assigns a number to any polyhedron—a surface, such as that of a cube, made up of polygons that meet along lines and at corner points. The Euler characteristic is easy to compute: Just add up the number of polygons, subtract the number of lines, and add the number of corner points. For example, a cube is made up of 6 square faces, 12 line edges, and 8 corners, so its Euler characteristic is 6 – 12 + 8 = 2.

The Euler characteristic is, remarkably, the same for all shapes with the same topology. For example, a hollow cube, tetrahedron, and dodecahedron each has an Euler characteristic equal to 2.

Mathematicians are now finding that the Euler characteristic and a more complex topological tool called homology can solve many problems about wireless sensor networks. Homology calculates how many holes a shape has and distinguishes between holes of different dimensions—a pinprick in a sheet of paper as compared to the interior of a balloon, for example. It also sheds light on how pieces—triangles or tetrahedrons, for instance—with different dimensions fit together to form an overall shape.

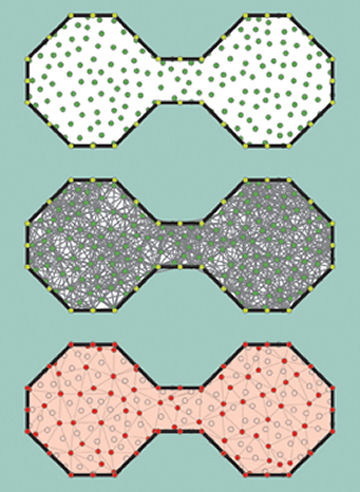
Like the Euler characteristic, homology works best on shapes built up out of what topologists call simplices, namely, corner points, lines, polygons, and their higher-dimensional analogs—objects that are hard to visualize but can be precisely described using mathematical formulas. Accordingly, to apply the power of these topological tools to wireless sensor networks, Ghrist and his collaborators put simplices together into a theoretical shape, called the Rips complex, that captures the intricacies of how the sensors communicate with each other.

In the Rips complex, named after mathematician Eliyahu Rips of the Hebrew University in Jerusalem, each sensor is represented by a corner point, and two points are connected by a line if their sensors are within communication range of each other.

When three sensors are within range of each other, the Rips complex includes a triangle with the three sensors at its corners. Similarly, when four sensors are within range, the Rips complex includes a tetrahedron. More generally, when n sensors are within range, the complex includes an (n–1)-dimensional simplex with those n corners.

In this way, the Rips complex contains all the information about clusters of sensors that can talk to each other. Its topology, researchers are finding, can uncover the hidden structure of wireless sensor networks.

Triangular coverage

Ghrist and his collaborator Vin de Silva of Pomona College in Claremont, Calif., have used the Rips complex to tackle a basic question about sensor networks: If you scatter a bucket of smart-dust particles over a field, how do you know whether their combined sensory range covers the entire region?

Today, engineers typically deal with this problem by equipping each sensor with a global-positioning device that can report its location. This approach works well for the small-scale networks currently in use, which might number a few hundred sensors. But developing miniature global-positioning devices for large-scale networks may be prohibitively expensive.

“We’re trying to prepare for the day—and it’s coming very soon—when we have millions of sensors distributed,” Ghrist says.

Many sensor-network engineers, Ghrist says, have assumed that it’s impossible to deduce the structure of a network without knowing where every sensor is. “If you don’t have the sensors’ coordinates, at first, it doesn’t seem as if you can do much,” Ghrist says.

Yet in the Dec. 1, 2006 International Journal of Robotics Research, Ghrist and de Silva showed how to use the homology of the Rips complex to figure out whether a network has full coverage. They needed to know only which sensors were within range of each other, not where each sensor was.

For the purposes of network coverage of, say, a field of corn, the researchers considered the triangles of the Rips complex. Each triangle represents a patch of the field that is completely within range of the three sensors at the triangle’s corners. The researchers asked, “When the triangles are pieced together, does the resulting quilt cover the field or leave holes?”

For a field whose perimeter is marked by sensors that are within range of their neighbors, Ghrist and de Silva have shown that unless the two-dimensional homology computation for the Rips complex comes out to zero, the triangles fully cover the field. In this case, the homology calculation not only guarantees coverage but also describes the most economical collection of triangles that covers the field. Only the sensors at the corners of the triangles in that collection need operate. Any other sensors are redundant and may be put in sleep mode, saving precious battery power.

“This is a big deal because if you have millions of sensors, you want to conserve their batteries as long as you can,” Ghrist says.

If the network has small gaps in coverage, the homology computation flags the sensors that border the gaps. Engineers then have various options, such as moving sensors into the gap or turning up the power of nearby sensors so that they each report on a larger area. “We can tell you exactly which sensors need to ramp up power, and by how much, to guarantee that the holes are filled,” Ghrist says.

Unlike the Euler characteristic, homology is far from straightforward to calculate. Ten years ago, Ghrist says, the homology calculations necessary for large sensor networks would have been impossible. However, with recent advances in homology algorithms and computer speed, a standard laptop can now compute the homology of a network of 10,000 sensors in less than a second.

Ali Jadbabaie, an engineer at the University of Pennsylvania in Philadelphia, has recently taken these homology algorithms a step farther. With his method, the sensors themselves compute the network’s homology by communicating with their neighbors, rather than by relaying information to a base station. “This is part of a drive toward more and more autonomy for sensor networks,” he says.

Jadbabaie’s algorithm can even handle situations in which the sensors’ positions are changing—if they are attached to animals, for instance, or blown about by the wind. “We can verify on the fly, in real time, whether you’re covering all the holes,” he says.

The topological approach currently makes several assumptions that don’t usually hold true in the physical world, cautions Gaurav Sukhatme, who studies sensor networks at the University of Southern California in Los Angeles. For instance, the approach often assumes that a sensor detects a circular region with a sharp boundary. Real-world sensors are frequently blocked by obstacles in some directions, and their sensing ranges tend to die off gradually rather than end abruptly.

“That said, you have to begin somewhere,” Sukhatme says. “It’s not unreasonable to start with these simplified models and then chip away at the constraints to see which can be removed. I think it’s an incredibly promising start.”

Counting games

Topology is also being applied to handle the data that sensor networks generate. For example, imagine that engineers are monitoring boat traffic because they want to know how many vessels are in a harbor at any moment. The engineers are using simple sensors that can keep track of how many, but not what kinds of, boats that they see. “If you’ve got two nearby sensors that each see three targets, you don’t know if they’re seeing the same three [boats] or, say, two the same and one different,” Ghrist says.

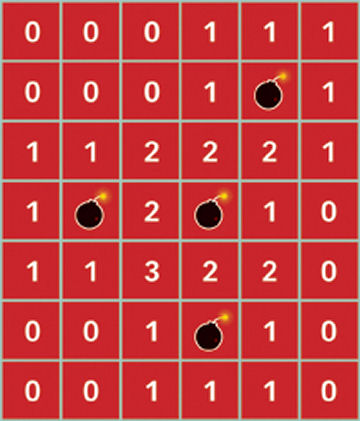
Ghrist likens the counting problem to that faced by players of Minesweeper, a popular computer game in which land mines are hidden in certain squares of a grid. Clicking on a square displays the number of mines in adjacent squares, unless the square itself hides a mine, in which case the player has lost the game.

In the Minesweeper scenario, it’s easy to calculate the total number of mines from the individual counts contributed by the squares. Eight neighboring squares count each mine, so the total number of mines is the sum of all the counts divided by eight. This method works as long as no mines border each other or the outer edges of the grid.

Real-world counting problems are considerably more unruly. Instead of each target triggering the same number of nearby sensors, different targets may have different impacts. In the harbor scenario, for example, a giant cruise ship might get counted by hundreds of sensors, while a dinghy might get counted by just a few.

Ghrist and Yuliy Baryshnikov of Bell Labs in Murray Hill, N.J., are using topological techniques to make inroads into this problem. “Our results are extremely robust,” Ghrist says. “We make very few assumptions about the system’s capabilities.”

Their theorem makes only one assumption about the targets: that the region from which a given target is visible is always a contractible shape, meaning that it could shrink to a single point without tearing or otherwise changing the shape’s topology.

The trick to counting the targets is to figure out a way to integrate all the sensors’ counts so that each target contributes equally to the total, just as each land mine contributes eight counts to the total in Minesweeper. Ghrist and Baryshnikov find that this can be accomplished without knowing how the targets vary in size or shape.

The Euler characteristic holds the key. Any contractible shape, for instance, the area from which a boat is visible, has an Euler characteristic of 1. Thus, adding up all the Euler characteristics gives the total number of boats. At first glance, this may seem circular because the number of boats isn’t known.

However, Ghrist and Baryshnikov have shown that it’s possible to calculate this sum using a variation of the Euler characteristic that counts the points, lines, and other simplices in the Rips complex not just once each but according to how many boats that each sensor can see. For example, if a given sensor can see five targets, it gets counted five times. Other simple rules apply to the lines and higher-dimensional simplices of the Rips complex.

This Euler-characteristic sum yields the total number of targets. The sensors can collectively carry out the calculations by comparing boat counts with those of their neighbors and by performing some straightforward arithmetic.

“There’s no complicated homology computation here,” Ghrist says. “This should be very implementable using simple sensors.”

Topological methods are expected to be useful to a host of other sensor-network problems. “I think mathematicians are really starting to take seriously the possibility that they could help us,” says Daniel Koditschek, who studies robotics and sensor networks at the University of Pennsylvania. “It’s extremely exciting.”

Sensor networks complicated enough to require topological analysis are right around the corner, Ghrist predicts.

“The field of sensor networks is changing very rapidly, with the kinds of stuff we’re able to build growing at an exponential rate,” he says. “We want to make sure that when these networks come into existence, the math is there and ready to use.”