“It was the last day of the 1999th year of our era. The pattering of the rain

had long ago announced nightfall; and I was sitting in the company of my
wife, musing on the events of the past and the prospects of the coming
year, the coming century, the coming Millennium.”
Those words appear near the beginning of the 15th chapter of a remarkable
book titled Flatland: A Romance of Many Dimensions.
Written in 1884 by Edwin A. Abbott (1838–1926), this slim volume has long
served as a doorway to the fourth dimension and beyond for many explorers
of geometry. The books central figure and narrator, “A Square,” takes
visitors into a two-dimensional world where a race of rigid geometric forms
live and love, work and play.
Like shadows, the denizens of Flatland freely flit about on the surface of
their world but lack the power to rise above or sink below it. All Flatlands
inhabitants–straight lines, triangles, squares, pentagons, and other
figures–are trapped in their planar geometry.
On the surface, Abbotts narrative appears to be simply an entertaining tale
and a clever mathematics lesson. From Flatlands beguiling text and quaint
drawings, readers can begin to imagine the strictly limited vistas open to
those trapped in a low-dimensional realm.
Flatland is also a sharply delineated satire that reflects widely debated
social issues in Victorian Britain. Abbott was a strong advocate of womens
rights, and he couldnt resist taking a satirical swipe at his class-conscious
societys attitudes toward women. Flatland women are merely Straight
Lines. Lower-class men are Isosceles Triangles; Squares make up the
professional class; Nobles are regular polygons with six or more sides; and
Priests, the highest-ranking members, are Circles.
“[A] Woman is a needle; being, so to speak, all point, at least at the two
extremities,” A Square comments. “Add to this the power of making herself
invisible at will, and you will perceive that a Female, in Flatland, is a
creature by no means to be trifled with.”
Nonetheless, Flatland women also are judged “devoid of brain-power, and
have neither reflection, judgment nor forethought, and hardly any memory.”
In this planar world, men believe that educating women is wasted effort and
that communication with women must occur in a separate language that
contains “irrational and emotional conceptions” not otherwise found in male
vocabulary.
When he wrote Flatland, Abbott was headmaster at the City of London
School, an institution that prepared middle-class boys for places at
universities such as Cambridge. He produced dozens of books, including
school textbooks, historical and biblical studies, theological novels, and a
well-regarded Shakespearean grammar that strongly influenced the study of
the Bards plays.
At first glance, Flatland appears out of place within this collection, but a
closer look shows that it combines elements of Abbotts broad range of
interests, from the reform of mathematics education to the nature of
miracles.
Abbott was a member of a group of progressive educators who sought
changes in the mathematics requirements for university entrance, which at
that time included memorization of lengthy proofs in Euclidean geometry.
Abbotts group considered such exercises a waste of time and felt that they
narrowed the study of geometry unnecessarily.
Abbotts interest in higher dimensions was also anomalous. Despite evident
public curiosity at the time about the concept of a fourth spatial dimension,
the mathematics establishment in Great Britain generally refused to admit
that higher-dimensional geometries were even conceivable. Conservative
mathematicians maintained that such concepts would call into question the
very existence and permanence of mathematical truth, as so nobly
represented by Euclidean geometry.
Abbott challenged such a narrow viewpoint and deliberately called Flatlands
university “Wentbridge”–a sly dig at Cambridge.
Flatland also represented one of Abbotts attempts to reconcile scientific
and religious ideas and to illuminate the relationship between material proof
and religious faith.
In the New Years Eve, 1999, episode, A Square receives a visit from a
ghostly sphere, who tries to demonstrate to the bewildered Flatlander the
existence of Spaceland and a higher dimension.
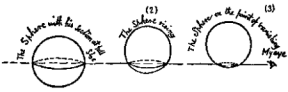
The visiting sphere argues that he is a “Solid” made up of an infinite number
of circles, varying in size from a point to a circle 13 inches across, stacked
one on top of the other. In Flatland only one of these circles is visible (as a line) at any
given moment. Rising out of Flatland, the sphere looks like a line that gets
shorter and shorter until it finally dwindles to a point, then vanishes
altogether.
When this vanishing trick fails to persuade A Square that the sphere is truly
three-dimensional, the visiting sphere tries a more mathematical argument.
A single point, being just a point, he insists, has only one terminal point. A
moving point produces a straight line, which has two terminal points. A
straight line moving at right angles to itself sweeps out a square with four
terminal points.
Those are all conceivable operations to a Flatlander. Inexorable
mathematical logic forces the next step. If the numbers 1, 2, and 4, are in a
geometric progression, then 8 follows. Lifting a square out of the plane of
Flatland ought to produce something with eight terminal points.
Spacelanders call it a cube. The argument opens a path to even higher
dimensions.
After a harrowing but eye-opening adventure in Spaceland, A Square
awakes on New Years Day, 2000, refreshed and filled with an evangelical
fervor to proclaim and propagate the Gospel of Three Dimensions. Sadly, no
one takes him seriously, and he ends up in prison for his beliefs.
Through mathematical analogy, Abbott sought to show that establishing
scientific truth requires a leap of faith and that, conversely, miracles can be
explained in terms that dont necessarily violate physical laws. Miracles
could be shadows of phenomena beyond everyday experience or intrusions
from higher dimensions, he argued.
Flatland raises the fundamental question of how to deal with something
transcendental, especially when recognizing that you would never be able to
grasp its full nature and meaning. Mathematicians face such a challenge
when they venture into higher dimensions. How do they see
multidimensional objects? How do they organize their observations and
concepts? How do they communicate their insights?
Flatland serves as a provocative and informative guidebook for pondering
those questions.
Happy New Year!






