One tradition that flourished 200 years ago in Japan, during its period of isolation from the western world, involved Euclidean geometry. Scholars and others would inscribe geometric problems on wooden tablets, then hang the tablets under the eaves of Shinto shrines and Buddhist temples as offerings. Such a tablet is called a sangaku, which means “mathematical tablet” in Japanese.

More than 800 tablets have survived. Many of them feature drawings and problems that concern tangent circles.
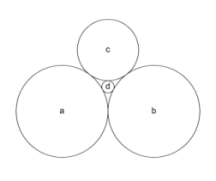
Here’s one example. Suppose three circles are tangent to one another and rest on a base line. Find a relationship among the radii of the three circles.
Problems involving tangent circles can often be solved using the Descartes circle theorem, named for French mathematician René Descartes (1596–1650). In a letter of November 1643 to Princess Elisabeth of Bohemia, Descartes developed a formula relating the curvatures of four circles, each of which touch all of the other three. He defined the curvature (or bend) of a circle as the reciprocal of its radius. Hence, if the radius of a circle is one-fifth (1/5) that of another, its curvature is 5 times that of the larger circle.
Given four mutually tangent circles with curvatures a, b, c, and d, the Descartes circle equation specifies that 2(a2 + b2 + c2 + d2) = (a + b + c + d)2.
The same formula holds for three touching circles nested within a fourth circle. In this case, however, the curvature of the outer circle is negative, because the other circles touch it from the inside rather than the outside. The formula also applies to configurations in which one or two of the touching circles are replaced by straight lines. A line is considered a circle with infinite radius and zero curvature.
Given three tangent circles, there are precisely two additional circles that are tangent to all three. If the original circles have curvatures a, b, and c, and the additional circles have curvatures d and d’, the following simple relationship holds: d + d’ = 2(a + b + c).
Interestingly, Descartes considered only one of the possible circle configurations, and his proof of the curvature relations was incomplete. In 1826, mathematician Jakob Steiner (1796–1863) independently discovered and proved the same result, around the same time that Japanese scholars were posing questions about tangent circles.
In 1842, Philip Beecroft, an English amateur mathematician, rediscovered the Descartes circle formula. Then it was discovered again in 1936 by Frederick Soddy (1877–1956), who had won a Nobel prize in 1921 for his discovery of isotopes.
Soddy expressed the theorem in the form of a poem, “The Kiss Precise,” which was published in the journal Nature. Here’s a portion of one verse:
Four circles to the kissing come,
The smaller are the benter.
The bend is just the inverse of
The distance from the centre. . . .
The sum of the squares of all four bends
Is half the square of their sum.
In another verse, Soddy announced his discovery of the analogous formula for five spheres in three dimensions.
The sphere is much the gayer,
And now besides the pair of pairs
A fifth sphere in the kissing shares.
In the latest twist, statistician Allan R. Wilks and his collaborators at AT&T Labs in Florham Park, N.J., have found a remarkable formula relating the curvatures and coordinates of tangent circles. They have also extended these results to spheres and higher-dimensional analogs of circles and to circles on hyperbolic and spherical surfaces.
Apollonius of Perga (c. 260–190 B.C.) pondered tangent circles more than 2,000 years ago. They have long been a staple of geometry textbooks and the subject of countless exercises, and they continue to fascinate.






