“A man, a plan, a canal–Panama.”

This statement is a famous example of a palindrome–a phrase that reads the same forward or backward. Inventive wordsmiths and puzzlists have come up with all sorts of words, sentences, and even paragraphs that have this property.
The term palindrome can also be applied to whole numbers, such as 1881, that are unchanged when the digits are reversed.
The topic of number palindromes comes up in an entertaining new book called TriMathlon: A Workout Beyond the School Curriculum, published by A K Peters. Written by Judith D. Sally of Northwestern University and Paul J. Sally Jr. of the University of Chicago, the book offers exercises, investigations, and games to challenge young readers in areas of number theory and geometry. The palindrome material is in the intermediate “bike” section, which provides projects involving numbers and symmetry.
When dates are expressed in terms of just numbers, you can look for dates that are palindromes. For example, if you let the first two digits represent the month, the second pair of digits represent the day, and the last four represent the year, the date Oct. 2, 2001, expressed as 10022001, is an eight-digit palindrome. Can you find the next one?
In TriMathlon, the mathlete begins with a guided search for all palindromes of five or fewer digits. This leads to the “reverse-and-add rule.”
Only nine two-digit numbers are palindromes. However, if you start with a two-digit number that is not a palindrome, try reversing the digits to get a new number, then add the new number to the old. If you try it with 25, the result (25 + 52 = 77) is a palindrome.
Does the rule always work? It does for 13, 45, and 56. But it doesn’t work for 67 (67 + 76 = 143). Why not try “reverse-and-add” again? This time, the result (143 + 341 = 484) is a palindrome. For 68, you need three steps to get a palindrome.
Mathematicians have conjectured that a palindrome always results after a finite number of additions for any positive integer of two digits or more.
There’s much more in the chapter on palindromes, including a two-digit palindrome game and other activities.
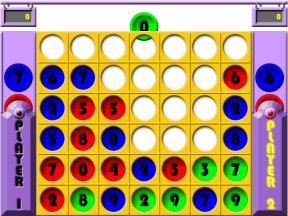
The Web site accompanying the book (http://www.trimathlon.com/) also features a two-player game involving number palindromes. Called “DropDigitDrop,” it resembles a game known as “Connect Four,” a kind of vertical tic-tac-toe, in which players take turns dropping colored disks into slots at the top of a seven-by-seven grid to try to get four of the same color in a row horizontally, vertically, or diagonally.
In the palindromic, two-player version, players have colored disks labeled with numbers. On each turn, a player chooses one of two randomly presented colored disks and drops the disk into one of seven slots. Every time a player completes a palindrome, the disks representing that palindrome disappear from the grid, and he or she scores points depending on the palindrome’s length. A player scores bonus points when the disk colors also make a palindrome (for example, red-green-blue-green-red). A game ends when the grid is full, and the player with more points wins. The game’s random element keeps it interesting.
In the one-person game (versus the computer), a player progresses from level to level, starting with just one color and three different digits. The game ends when either the computer scores more points than you do in a given round, or you reach a stage where you have more points and force an end by filling the grid.
If you have a Web browser that handles Shockwave, you can try the game yourself at http://www.trimathlon.com/dropdigitdrop.asp.






