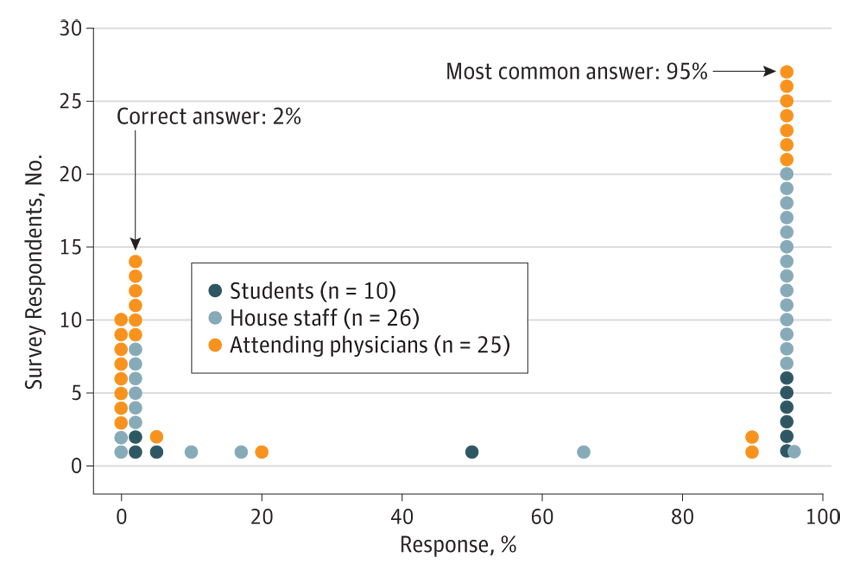
Of 61 physicians, hospital staff and medical students asked, "If a test to detect a disease whose prevalence is 1 out of 1,000 has a false positive rate of 5 percent, what is the chance that a person found to have a positive result actually has the disease?" only 14 gave the correct answer — 2 percent.
A.K. Manrai et al./JAMA Internal Medicine 2014
- More than 2 years ago
Imagine a hypothetical baseball player. Call him Alex. He fails a drug test that is known to be 95 percent accurate. How likely is it that he is really guilty?
If you said 95 percent, you’re wrong. But don’t feel bad. It puts you in the company of a lot of highly educated doctors.
OK, it’s kind of a trick question. You can’t really answer it without knowing some other things, such as how many baseball players actually are guilty drug users in the first place. So let’s assume Alex plays in a league with 400 players. Past investigations indicate that 5 percent of all players (20 of them) use the illegal drug. If you tested them all, you’d catch 19 of them (because the test is only 95 percent accurate) and one of them would look clean. On the other hand, 19 clean players would look guilty, since 5 percent of the 380 innocent players would be mistakenly identified as users.
So of all the players, a positive (guilty) test result would occur 38 times — 19 truly guilty, and 19 perfectly innocent. Therefore Alex’s positive test means there’s a 50-50 chance that he is actually guilty.
Now if these mathematical machinations mattered only for baseball, it wouldn’t be worth blogging about. But the same principles apply to medical screening tests. For decades, doctors and advocacy groups have promoted screening tests for all sorts of diseases without putting much thought into the math for interpreting the test results.
Way back in 1978, one study found that many doctors don’t understand the relationship between the accuracy of a test and the probability of disease. But those doctors probably went to med school in the ’60s and weren’t paying much attention. And there were no blogs or Twitter to disseminate important medical information back then. So some Harvard Medical School researchers recently decided to repeat the study. They posed the question in exactly the same way: “If a test to detect a disease whose prevalence is 1 out of 1,000 has a false positive rate of 5 percent, what is the chance that a person found to have a positive result actually has the disease?” The researchers emphasized that this was just for screening tests, where doctors had no knowledge of anyone’s symptoms.
Of 10 medical students given the quiz, only two got the right answer. So we can hope that the other eight will flunk medical school and never treat any patients. But of 25 “attending physicians” given the question, only six got the right answer. Other hospital staff (such as interns and residents) didn’t do any better.
Among all the participants, the most common answer was 95 percent, the test’s accuracy rate. But as with the hypothetical drug test, the test’s actual “positive predictive value” for how many people really had the disease was much lower, in this case only about 2 percent. (If only 1 in a 1,000 people have the disease, testing 1,000 people would produce about 50 false positives and 1 correct identification; 1 divided by 51 is 1.96 percent.)
“Our results show that the majority of respondents in this single-hospital study could not assess PPV in the described scenario,” Arjun Manrai and collaborators wrote in a research letter published April 21 in JAMA Internal Medicine. “Moreover, the most common error was a large overestimation…, an error that could have considerable impact on the course of diagnosis and treatment.”
Really, you don’t want a doctor who tells you it’s 95 percent likely that you’re toast when the actual probability is merely 2 percent.
It’s natural to wonder, though, whether these hypothetical exercises ever apply to real life. Well, they do, in everything from prostate cancer screening to mammography guidelines. They also apply to news reports about new diagnostic tests, an area in which the media are generally not very savvy.
One recent example involved Alzheimer’s disease. In March, the journal Nature Medicine published a report about a test of blood lipids. It predicted the imminent arrival (within two to three years) of Alzheimer’s (or mild cognitive impairment) with over 90 percent accuracy. News reports heralded the 90 percent accuracy of the test as though it were big deal. But more astute commentary pointed out that such a 90 percent accurate test would in fact be wrong 92 percent of the time.
That’s based on an Alzheimer’s prevalence in the population of 1 percent. If you test only people over age 60, the prevalence rate goes up to 5 percent. In that case a positive result with a 90 percent accurate-test is correct 32 percent of the time. “So two-thirds of positive tests are still wrong,” pharmacologist David Colquhoun of University College London writes in a blog post, where he works out the math in detail for use in evaluating such screening tests.
Neither the scientific paper nor media reports pointed out the fallacy in the 90 percent accuracy claim, Colquhoun noted. There seems to be “a conspiracy of silence about the deficiencies of screening tests,” he comments. He suggests that researchers seeking funding are motivated to hype their results and omit mention of how bad their tests are, and that journals seeking headlines don’t want to “pour cold water” on a good story. “Is it that people are incapable of doing the calculations? Surely not,” he concludes.
But many doctors and journal editors and journalists surely aren’t capable (or at least haven’t tried) to do the calculations. As the Harvard researchers point out in JAMA Internal Medicine, efforts to train doctors about statistics need improvement.
“We advocate increased training on evaluating diagnostics in general,” they write. “Specifically, we favor revising premedical education standards to incorporate training in statistics in favor of calculus, which is seldom used in clinical practice.”
Statistical training would also be a good idea for undergraduate journalism programs. And it should be mandatory in graduate level science journalism programs. It’s not — perhaps because many students in such programs already have an advanced science degree. But that doesn’t mean that they actually understand statistics. Even if they’ve taken a statistics course. Science journalists really need a course in statistical inference and evaluating evidence, designed specifically for reporting on scientific studies. Maybe in my spare time I could put something like that together. But I’d probably have to hype it to get funding.
Follow me on Twitter: @tom_siegfried
Editor’s Note: This story was updated on April 23, 2014, to correct the title and affiliation of David Colquhoun.






