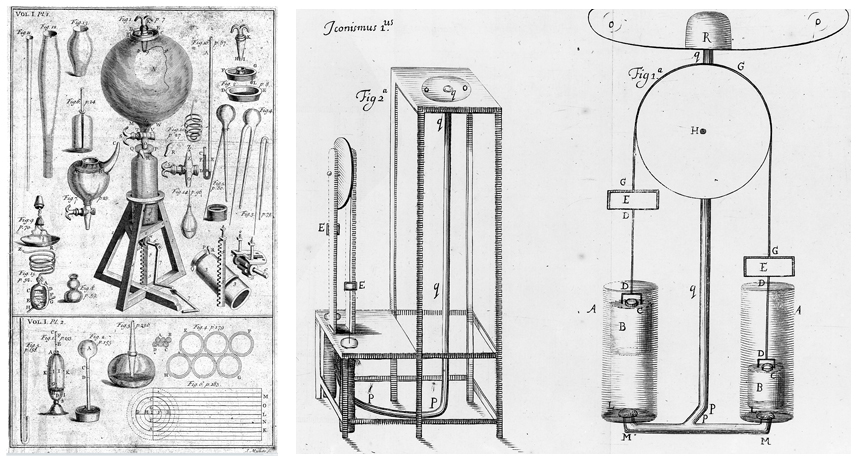
Seventeeth-century physicist and inventor Robert Boyle made a point to communicate the details of his experiments creating a vacuum with an air pump (his first and third attempts are illustrated here) so others could reproduce his results. Statisticians have devised a new way to measure the evidence that an experimental result has really been reproduced.
Wellcome Library, London (CC BY 4.0)
- More than 2 years ago
Whether in science or in courtrooms, drawing correct conclusions depends on reliable evidence. One witness is not enough.
Robert Boyle, one of the founding fathers of modern experimental science, articulated that science/law analogy back in the 17th century.
“Though the testimony of a single witness shall not suffice to prove the accused party guilty of murder; yet the testimony of two witnesses . . . shall ordinarily suffice to prove a man guilty,” Boyle wrote. In the same way, he said, a scientific experiment could not establish a “matter of fact” without multiple witnesses to its result.
So in some of his famous experiments creating a vacuum with an air pump, Boyle invited prominent spectators, “an illustrious assembly of virtuosi,” to attest to the fact of his demonstrations. Boyle realized that such verification could also be achieved by communicating the details of his methods so other experimenters could reproduce his findings. Since then, the principle that experiments should be reproducible has guided the process of science and the evaluation of scientific evidence.
“Replicability has been the cornerstone of science as we know it since the foundation of experimental science,” statistician Ruth Heller and collaborators write in a recent paper.
For quite a while now, though, it seems as if that cornerstone of science has been crumbling. Study after study finds that many scientific results are not reproducible, Heller and colleagues note. Experiments on the behavior of mice produce opposite results in different laboratories. Drugs that show promise in small clinical trials fail in larger trials. Genes linked to the risk of a disease in one study turn out not to have anything to do with that disease at all.
Part of the problem, of course, is that it’s rarely possible to duplicate a complicated experiment perfectly. No two laboratories are identical, for instance. Neither are any two graduate students. (And a mouse’s behavior can differ depending on who took it out of its cage.) Medical trials test different patients each time. Given all these complications, it’s not always obvious how to determine whether a new experiment really reproduces an earlier one or not.
“We need to have an objective way to declare that a certain study really replicates the findings in another study,” write Heller, of Tel-Aviv University in Israel, and collaborators Marina Bogomolov and Yoav Benjamini.
When comparing only two studies, each testing only one hypothesis, the problem is not severe. But in the era of Big Data, multiple studies often address multiple questions. In those cases assessing the evidence that a result has been reproduced is tricky.
Several small studies may suggest the existence of an effect — such as a drug ameliorating a disease — but in each case the statistical analysis can be inconclusive, so it’s not clear whether any of the studies reproduce one another. Combining the findings from all the studies, a procedure known as meta-analysis, may produce strong enough data to conclude that the drug works. But a meta-analysis can be skewed by one study in the group showing a really strong effect, masking the fact that other studies show no effect (and thus do not reproduce each other).
“A meta-analysis discovery based on a few studies is no better than a discovery from a single large study in assessing replicability,” Heller and colleagues point out.
Their approach is to devise a new measure of replicability (they call it an r-value) for use in cases when multiple hypotheses are tested multiple times, an especially common situation in genetics research. When thousands of genes are tested to see if they are related to a disease, many will appear to be related just by chance. When you test again, some of the same genes show up on the list a second time. You’d like to know which of them counts as a reliable replication.
Heller and colleagues’ r-value attempts to provide a way of quantifying that question. They construct an elaborate mathematical approach, based on such factors as the number of features tested in the first place and the fraction of those features that appear not to exert an influence in either the first or follow-up study. Tests of the r-value approach show that it leads to conclusions that differ from standard methods, such as genome-wide association studies. In the GWAS approach, hundreds of thousands of genetic variations are investigated to see if they show signs of being involved in a disease. Follow-up tests then determine which of the candidate variations are likely to be truly linked to the disease.
A GWAS analysis of Crohn’s disease, for instance, tested over 600,000 genetic variations in more than 3,000 people. A follow-up analysis re-examined 126 of those genetic variations. Using the r-value method, Heller and colleagues determined that 52 of those variations passed the replication test. But those 52 were not the same as the 52 most strongly linked variations identified by the standard GWAS method. In other words, the standard statistical method may not be providing the best evidence for replication.
But as Heller and colleagues note, their method is not necessarily appropriate for all situations. It is designed specifically for large-scale searches when actual true results are relatively rare. Other approaches may work better in other circumstances. And many other methods have been proposed to cope with variations on these issues. Different methods often yield different conclusions. How to know whether a result has really been reproduced remains a weakness of the scientific method.
Of course, even in Boyle’s time, though, reproducibility wasn’t so simple. Boyle lamented that, despite how carefully he wrote up his reports so that others could reconstruct his apparatus and reproduce his experiments, few people actually tried.
“For though they may be easily read,” Boyle wrote, “yet he, that shall really go about to repeat them, will find it no easy task.”
Follow me on Twitter: @tom_siegfried






