A map can show much more than rivers, roads, and political boundaries. It can express an attitude. Saul Steinberg’s famous New Yorker cover illustration, called “View from 9th Avenue,” shows a foreshortened map of New York City and its environs. Beyond the city’s avenues and the Hudson River, Steinberg’s map looks westward toward vaguely defined regions: Jersey, the rest of the United States, the Pacific Ocean, and a barely visible Asia and Europe. The map neatly encapsulates a Manhattanite’s self-centered perspective on the world.
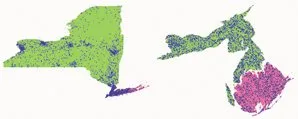
A map can also illuminate the way people live. It can incorporate census results, disease incidence, or the number of telephones in use. A simple color code, for example, can show where the incidence of a particular disease is high and where it’s low.
Such representations, however, can be misleading. Inevitably, cities would show a higher incidence than rural areas merely because the former have larger populations. Plotting per capita incidence takes care of that problem but discards information about where most of the cases occurred.
One solution is to take out variations in population density but still show how many cases occur in each region. This can be done on a distorted map in which the sizes of geographic regions appear in proportion to their populations, whether it’s people or goods, or other items. Such a map is known as a cartogram.
Constructing a usable cartogram is challenging. The computer methods currently available sometimes produce maps with overlapping regions or weird distortions. In some cases, the maps are so highly skewed that they’re difficult to read or interpret. Moreover, it can take hours of computer time to produce a single cartogram.
Now, two researchers have turned to the physics of diffusion to develop a new, speedy technique for generating cartograms by computer. “Our method is conceptually simple and produces useful, elegant, and easily readable maps,” say Mark E.J. Newman and Michael T. Gastner of the University of Michigan in Ann Arbor. They describe their procedure in the May 18 Proceedings of the National Academy of Sciences (PNAS).
There’s an urgent need for a method that really works, says geographer Daniel Dorling of the University of Sheffield in England. The algorithm proposed by Newman and Gastner may “prove to be of huge value in cartography worldwide,” he suggests.
Perfect distortion
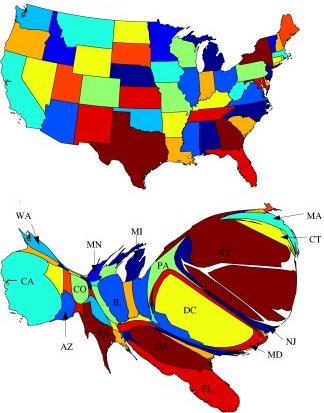
A geographic map of the continental United States shows a patchwork of states of varying sizes and shapes. Creating a new map in which the area of each state is proportional to its population requires enlarging densely populated states and shrinking sparsely populated ones. On such a map, populous New Jersey would loom large despite its relatively small area and vast Wyoming would turn tiny.
Mathematically, it can be shown that there are infinitely many ways to perform such a transformation, even while making sure that the total area and the basic connectedness, or topology, of the map don’t change. With such leeway, geographers and other researchers have proposed many different methods. Dorling himself has invented several ingenious techniques for producing cartograms, but each one has disadvantages.
The “perfect” cartogram, says Dorling, would be one that also minimizes local distortion. “If you were to look in detail at a very small area of the cartogram, it should look very similar to a normal map,” he says. For example, Utah, Colorado, New Mexico, and Arizona meet at right angles on a standard map of the United States. These states should also come close to doing so on a cartogram.
Achieving such perfection would be difficult, so researchers have focused on making good-enough cartograms efficiently.
Newman and Gastner started with the observation that, on a population cartogram, the population is spread out evenly. The conversion of a geographic map into a cartogram reminded the physicists of diffusion—the process by which a gas spreads to fill available space until it has a uniform density throughout.
Applied to a map, there would be a flow from areas with high population densities to those with low densities. This flow would take any boundaries with it to create the new map.
Inspired by this analogy, Newman and Gastner turned to an equation that physicists use to describe diffusion. Starting with a mathematical description of the population density for a given map, they used a computer to solve the diffusion equation through a step-by-step process. The result: a map in which the population density is the same everywhere and that has no overlapping regions.
“The programming necessary to make this work is quite involved, so it took a while to produce the first maps,” Newman says. “Once we did, however, it rapidly became clear that this was a useful tool.”
It’s a little surprising that no one had thought to use this approach before. “Perhaps it’s reasonable to a physicist—diffusion is something physicists all study as undergraduates—but not to someone in cartography or geography, which is where most people working on this topic are coming from,” Newman says.
“The method of Newman and Gastner is elegant,” agrees geographer Waldo Tobler of the University of California, Santa Barbara, “but the mathematics is rather difficult.”
In the late 1960s, Tobler, who was then at the University of Michigan, was the first to propose a method for the automated computer generation of cartograms. In his original scheme, the initial map is divided into small rectangular or hexagonal cells. Each cell is independently enlarged or contracted to a size proportional to its population. The resized cells are then distorted so that corners match again. The sizing process is repeated again and again until the population density in the cells evens out.
It was an important first step, but Tobler’s method was quite slow and sometimes produced unfortunate distortions.
Other researchers tried to improve upon Tobler’s effort. One scheme, recently developed by Dorling, also divided a map into tiny cells. With each step of the procedure, cells lying near a boundary would be reassigned as required to meet population requirements. Populous areas would grow larger at the expense of less-populated areas.
Another method permitted the borders of cells to move in response both to space requirements and to theoretical forces exerted by other cells.
Although there were improvements in performance, no method completely solved the problem.
Skewed states
Newman and Gastner have tried out their diffusion method on population data from the 2000 U.S. census. To demonstrate the technique’s effectiveness and versatility, they created cartograms displaying the results of the U.S. presidential election of 2000, lung cancer rates among males in the state of New York, and the distribution of wire service news stories by state.
In the close contest between Republican George Bush and Democrat Al Gore, Newman and Gastner’s cartogram based on population density reveals a fairly even split. In contrast, using a standard geographic map and simply coloring in each state according to which candidate had received more votes there produces a much larger area in the Republican color—even though Gore finished slightly ahead in the popular vote.
“Clearly then, a simple map is a poor visual representation of the election results, in the sense that it is hard to tell which party got more votes by looking at the map,” Newman and Gastner say.
In each of their applications, the researchers had to decide what type of geographic area to choose as a basic unit. For example, in the United States, they could take the population of each state and distribute it uniformly over the state’s area, or they could do it county by county or census tract by census tract.
The choice of unit used to establish the so-called population-density function affects the amount of distortion in the resulting cartogram. For example, distributing a state’s population over its entire area generally produces a map with more recognizable features than does a county-by-county distribution, because cities cause substantial local distortions.
“Part of the art of making a good cartogram lies in shrewd decisions about the definition of the population-density,” Newman and Gastner say in their PNAS paper. Ultimately, the choice of population-density function is up to the user of the method, who must decide what particular features are most desirable in his or her application.
The Newman-Gastner technique generates a cartogram remarkably quickly. “Maps are complicated things, and any calculation takes quite a long time,” Newman says. “Our method . . . allows us to speed up the calculations a great deal and complete them in just seconds [rather than hours or days]. This makes a lot of difference to the usability of the method.”
The physicists also discovered that their method generates maps that are visually pleasing and easy to read. “If you have correctness, speed, and useful, readable maps, then you have pretty much everything a cartogram needs,” Newman says.
So far, Newman and Gastner have applied their technique only to standard examples. They plan to develop a software package that would permit geographers or cartographers to use the method on trickier, more interesting problems without having to write complex computer programs themselves.
Newman and Gastner are working to further increase the method’s speed. They are also considering the application of their tool on a global scale.
“We haven’t done anything larger than the United States, but that’s not because of scaling problems,” Newman says. “In fact, the U.S. maps were done on a 1,000-by-1,000 grid, so we already, in effect, had a million regions in those maps, and the calculations were still very quick.”
The challenge in creating maps of large portions of the world derives from Earth’s curvature. The method that Newman and Gastner used to flatten the area covered by the United States doesn’t work for the whole globe.
Going to larger areas “would involve rewriting our computer codes,” Newman says. Nonetheless, “in terms of running time, I see no reason why very large maps, including the entire world, should not be possible.”
Although Dorling praises the work of Newman and Gastner, he sees the need for additional research on methods for generating global cartograms to get closer to the best cartogram that is theoretically possible.
“Creating [perfect] cartograms remains an algorithmic puzzle,” he says. “I’ve been searching for 15 years to find a Ph.D. student willing to take this problem on. We now have the computational power—we lack the brains. The solution has probably already been found in another area.”
“One of the repeated lessons of the field of complex systems in which I work is that there are an awful lot of good ideas out there, and many of them are well known, but few of them are well known in every field,” Newman says. “So, people can make significant progress by applying an idea commonplace in one area to a field in which it has less, or no, currency.”






