- More than 2 years ago
Last April, the Genesis spacecraft began its journey home. It had been parked out in space collecting solar particles for 2 years. Yet even though its job was done, Genesis didn’t head straight home. Instead, it took a 3-million-mile detour, swinging past Earth to do a loop de loop around a distant point before flying back to Earth.

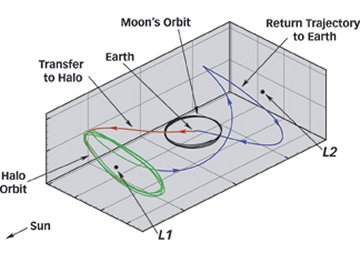
This circuitous route was no accident. The spacecraft had hopped aboard the interplanetary superhighway, a network of tubes crisscrossing through the solar system. By jumping from one tube to another at the solar system’s version of highway interchanges, a spacecraft can travel vast distances using practically no fuel.
“Genesis was the most efficient space mission ever flown,” says Jerrold Marsden, a mathematician at the California Institute of Technology in Pasadena who studies spacecraft trajectories.
A celestial superhighway sounds like the output of a science fiction writer’s overheated brain. Yet it’s reality, grounded in the competing gravitational tugs of the sun, Earth, and other solar system bodies. By studying the mathematics underlying subtle gravitational interactions, researchers are starting to create an atlas of this superhighway. Engineers are designing trajectories to send spacecraft coasting along these routes to make voyages that were previously unimaginable.
Traditionally, spacecraft have used fuel-guzzling engines to punch their way across the solar system, says Edward Belbruno, a mathematician at Princeton University who masterminded the first spacecraft journey along low-fuel highways in 1991. Travel on the interplanetary superhighway works with gravity, not against it, he explains.
“The old way is like using a 747 jet to blast through the sky,” Belbruno says. “The new way is like using a glider plane, which rides the natural currents and eddies of the air.”
Gravitational sweet spots
Engineers have traditionally pieced together a spacecraft’s path by considering the gravitational pulls between the spacecraft and just one other body at a time. To create trajectories for the Apollo lunar missions, for instance, engineers calculated how Earth’s gravity would affect the spacecraft at the beginning of its trip and how the moon’s gravity would affect the craft toward the end. Each of these interactions is considered a two-body problem because it asks how two objects—such as Earth and a spacecraft—behave if the only forces acting on them are each other’s gravity.
Isaac Newton solved the general two-body problem in the 17th century. He calculated that the two bodies rotate around their common center of gravity. By adding in the forces generated by a spacecraft’s thrusters, engineers have used Newton’s equations to design the spacecraft’s trajectory.
The paths that arise from this method tend to be direct but inefficient. “You just brute force your way there,” Marsden says. The spacecraft must expend much fuel to counterbalance the pulls of other celestial bodies.
Newton himself tried to analyze these other pulls, but he hit a wall when he tried to calculate how three objects would move under the influence of each other’s gravity. In the centuries that followed, this three-body problem became one of the most famous questions in mathematics. In the 1950s, mathematicians finally proved that it’s impossible to solve.
Nevertheless, over the centuries, mathematicians have gained traction in understanding a simplified version of the three-body problem that happens to be ideal for designing spacecraft trajectories. This restricted three-body problem asks, What happens to three bodies if two are massive but the third—say, a spacecraft—is so small that its gravitational pull on the other two is negligible?
In such a setup, the two large bodies—say, the sun and Earth—behave as in Newton’s two-body analysis, rotating around their common center of mass. In the case of Earth and the sun, this center of mass is buried deep inside the sun, creating the appearance that the sun is stationary and that Earth orbits it.
To visualize how the gravitational pulls of the sun and Earth will affect a spacecraft, mathematicians plot the three bodies using what’s called a rotating frame, a coordinate system that turns along with the sun and Earth. In these coordinates, the sun and Earth are always at the same two fixed points.
In the 18th century, European mathematicians Leonhard Euler and Joseph-Louis Lagrange discovered that in this rotating frame there are five gravitational sweet spots, now called Lagrange points. At these equilibrium points, the competing pulls on the third body balance each other, and the body remains motionless.
To find one of these Lagrange points, consider the line connecting the sun and Earth. At one point on this line, the gravitational pulls of the sun and Earth balance, so any object placed there should stay put. This equilibrium is unstable, like that of a marble poised on a mountain ridge. If the object is given even the slightest push, it will go zooming away from the equilibrium.
That analysis is incomplete because it ignores another pull. The centrifugal force, which pushes a person outward on a carousel, also pushes outward any objects in the rotating coordinate system. As a result, the true balance point between the sun and Earth, called L1, is closer to the sun than it would be without the centrifugal force.
The centrifugal force produces four additional equilibrium points. One, called L2, sits along the Earth-sun line on the far side of Earth, at the spot where the combined inward pulls of the sun and Earth balance the outward centrifugal push. An analogous point, L3, sits on the far side of the sun. Like L1, these two equilibriums are unstable.
Harder to visualize are L4 and L5, which sit at two points that complete equilateral triangles with the sun and Earth. L4 and L5 are stable equilibriums: An object placed at one of these points will tend to stay fixed.
The Lagrange points have captured the attention of both astronomers and amateur space enthusiasts. Because L1 offers an unobstructed view of the sun, it’s currently home to several sun-observing spacecraft, such as the Solar and Heliospheric Observatory. And L2, at which a telescope can always face away from both Earth and the sun, is an ideal spot for deep-space observatories. The Wilkinson Microwave Anisotropy Probe (WMAP), which measures the cosmic background radiation, is in orbit there. More fancifully, L3 is science fiction writers’ favorite spot to conceal a “Planet X,” since it’s always on the opposite side of the sun from Earth.
It’s the unstable Lagrange points—especially L1 and L2—that are most useful for designing spacecraft trajectories, according to Marsden. “In nature, unstable things are often more efficient than stable things,” he says.
Just as it’s possible to balance a pencil vertically on your hand—a highly unstable state—by gently wiggling your hand, it’s possible for a spacecraft to stick around an unstable Lagrange point using small rocket thrusts. But, it’s even easier for that craft to go swinging away into a different part of the solar system.
Tube hopping
In the late 19th century, French mathematician Henri Poincaré had an amazing insight. He realized that the restricted three-body problem displays sensitivity to initial conditions. That is, two objects that start out in nearly the same spot can go spiraling off into wildly different regions of space. Poincaré’s discovery gave birth to the mathematical field of chaos theory, which today encompasses a host of phenomena, from the weather to traffic patterns.
Despite this chaos, Poincaré found that it’s possible to organize similar paths through the three-body system into special surfaces. In the late 1960s, mathematicians Charles Conley of the University of North Texas in Denton and Richard McGehee of the University of Minnesota in Minneapolis built on this work to discover a collection of these special surfaces shaped like tubes. These spiral into or out of orbit around the unstable Lagrange points. If an object sits in one of these tubes, the natural gravitational pulls sweep it along, toward or away from the Lagrange points.
In 2000, Marsden and his collaborators showed that these tubes wind chaotically through space. Although chaos is a drawback when it comes to predicting the weather, from the point of view of designing spacecraft trajectories it’s great news. Near a Lagrange point, a spacecraft can use a tiny thrust to hop between tubes that snake off to completely different destinations.
These tubes make up the freeways of the interplanetary superhighway, so named by Marsden’s collaborator Martin Lo of NASA’s Jet Propulsion Laboratory (JPL) in Pasadena, Calif. However, the tubes of the five Lagrange points are just a small piece of the picture. After all, the restricted three-body problem can be applied not just to the sun and Earth but also to Earth and the moon, the sun and Jupiter, and many other pairs of large bodies. Each celestial pair produces its own Lagrange points and tubes. And “in remarkable coincidences all through the solar system,” Marsden says, many of these tubes link to form a network of intersecting highways.
Unlike terrestrial highway systems, the interplanetary superhighway is not static. The Earth-sun Lagrange points and tubes, for instance, are stationary only when considered in the Earth-sun rotating frame. In reality, the tubes flail about “like streams from a crazy garden sprinkler,” Marsden says, and the patterns of highway interchanges keep shifting.
To get from one tube to another, a spacecraft must hop on at exactly the right moment and at the right speed. Marsden says, “It’s like transferring between trains at a station with no platform. The other train had better get to the station at the exact time you arrive.” Fortunately, researchers can now use computers to chart when and where many of these highway interchanges materialize.
Exploring the superhighway
The three-body problem made its spacecraft trajectory debut in 1991, when Belbruno helped rescue the first Japanese mission to the moon. The Japanese spacecraft Hiten, while orbiting Earth, had ejected a basketball-size probe that was supposed to go into lunar orbit. Unfortunately, the probe was lost after its communications system failed. The much-larger Hiten, never intended for lunar orbit, lacked the fuel to reach the moon.
Five years earlier, Belbruno had used the dynamics of the three-body problem to design a hypothetical 2-year trajectory that rode gravitational currents from Earth to the moon without requiring fuel. He and James Miller of JPL put the idea to the test by modifying this trajectory into a 3-month path to the moon for Hiten.
“The route flew 1 million kilometers past the moon before falling down to it,” Belbruno recalls. “It allowed Hiten to ride a crest and get to the moon for free.”
More recently, the European Space Agency’s SMART-1 spacecraft followed Belbruno’s original 2-year trajectory to the moon, arriving there late last year.
Although Belbruno didn’t express his work in terms of tubes and highways, it laid the groundwork for subsequent mathematical explorations of the interplanetary superhighway. In the mid-1990s, a team led by Lo and Kathleen Howell of Purdue University in West Lafayette, Ind., built on these ideas to design a superhighway trajectory for Genesis, whose mission was to collect particles of the wind constantly emanating from the sun. In August 2001, Genesis rode a tube from Earth out to the Earth-sun L1, where it orbited five times, facing the sun. For its return journey, it followed a highway route that swung past the Earth-sun L2 and then coasted back to Earth.
After takeoff, Marsden says, Genesis used fuel only to stay balanced and make small adjustments to keep on course. That fuel amounted to just 4 percent of the craft’s total mass, says Shane Ross of the University of Southern California in Los Angeles, who worked with Lo and Howell. By contrast, previous missions, such as Galileo and the Apollo Lunar Lander, consumed from 40 percent to 60 percent of their weight in fuel.
It currently costs about $1 million to send just a pound of fuel to the moon, Belbruno says.
But perhaps more important, the interplanetary superhighway’s fuel efficiency enables researchers to construct space trajectories that would otherwise be infeasible. For instance, Marsden, Lo, and Ross worked out a potential tour of Jupiter’s moons that NASA has adapted for its planned Jupiter Icy Moons Orbiter (JIMO). Its launch is tentatively scheduled for 2012.
JIMO will exploit the linkages among the tubes of the planet and its four icy moons to leapfrog from one moon to the next, orbiting each in turn, to collect data on whether liquid oceans lurk under the moons’ surfaces. Previous missions to Jupiter have included only brief flybys of its moons because to slow down and go into orbit using conventional trajectories takes “a colossal amount of fuel,” Marsden says. “But using tube hopping, you can linger as long as you want at one of the moons and it doesn’t cost you more fuel,” he adds.
In addition to planning one-time missions along the superhighway, Marsden, Lo, and Ross, together with a NASA team, conceive of a permanent manned space station at the Earth-moon L1 point. Ross calls it the “nearest rest stop on the superhighway.” Astronauts could get there from Earth in days, and a spacecraft could travel in hours from the station to any point on the moon.
The main attraction of such a station, Ross says, is that each month the tubes from the Earth-moon L1 intersect tubes to the Earth-sun L1 and L2. Astronauts could travel to the station by conventional means. Once there, they could assemble, say, a deep-space telescope intended for the Earth-sun L2, then set it drifting along the tubes toward its final destination. Such telescopes could be larger and more delicate than those sent from Earth because they wouldn’t have to fit in a rocket and withstand the rigors of a launch. And if a telescope at the Earth-sun L2, such as WMAP, were to malfunction, it could simply ride a tube back to the lunar gateway station for servicing.
“It would be hard to send humans to the Earth-sun L2 to service a broken telescope because of the long transit time and the harsh radiation environment,” Ross says. “But it would be easy to bring the telescope back to the gateway station.”
It’s unlikely that astronauts themselves will ever ride the interplanetary superhighway, though they might someday guide telescopes on and off its entry ramps, says Wendell Mendell of NASA Johnson Space Center in Houston. Because the tubes follow such winding routes, trips along them tend to take a long time—compare Belbruno’s 2-year trajectory to the moon to the 4-day Apollo 11 mission, for instance. Using the tubes is like sending cargo down the Mississippi River on a barge, Mendell says. “It’s cheap but slow.”
For unmanned missions, the interplanetary superhighway’s potential is just starting to unfold, Marsden says. “I suspect that there are tubes connecting many more systems of moons and planets than we’ve discovered so far.”






