News in Brief Genetics

Scientists move closer to building synthetic yeast from scratch

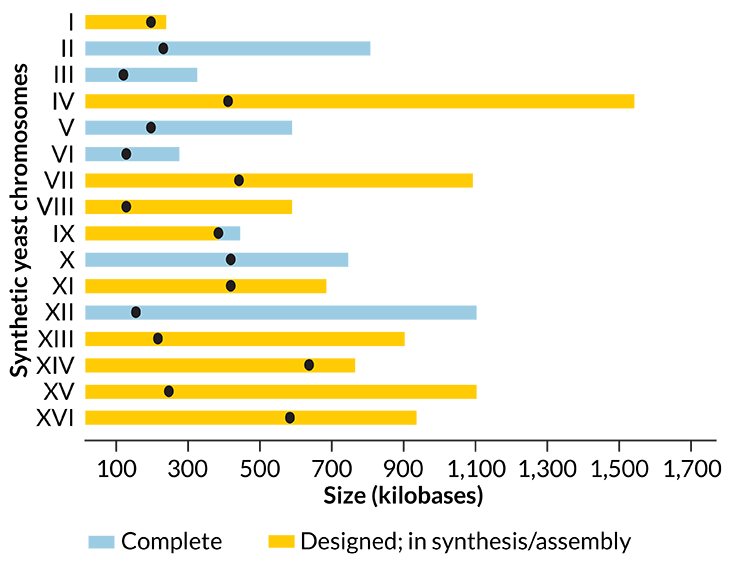
Five more chromosomes assembled, 10 to go

Saccharomyces cerevisiae yeast

BUDDING STAR  With five more synthetic chromosomes built, scientists are closer to creating a synthetic genome for Saccharomyces cerevisiae yeast (shown).

Mogana Das Murtey and Patchamuthu Ramasamy/Wikimedia Commons (CC BY-SA 3.0)

By Laurel Hamers

- More than 2 years ago

Synthetic yeast is on the rise.

Scientists have constructed five more yeast chromosomes from scratch.