- More than 2 years ago
Many people regard mathematics as the crown jewel of the sciences. Yet math has historically lacked one of the defining trappings of science: laboratory equipment. Physicists have their particle accelerators; biologists, their electron microscopes; and astronomers, their telescopes. Mathematics, by contrast, concerns not the physical landscape but an idealized, abstract world. For exploring that world, mathematicians have traditionally had only their intuition.
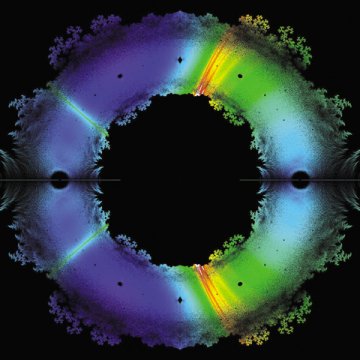
Now, computers are starting to give mathematicians the lab instrument that they have been missing. Sophisticated software is enabling researchers to travel further and deeper into the mathematical universe. They’re calculating the number pi with mind-boggling precision, for instance, or discovering patterns in the contours of beautiful, infinite chains of spheres that arise out of the geometry of knots.
Experiments in the computer lab are leading mathematicians to discoveries and insights that they might never have reached by traditional means. “Pretty much every [mathematical] field has been transformed by it,” says Richard Crandall, a mathematician at Reed College in Portland, Ore. “Instead of just being a number-crunching tool, the computer is becoming more like a garden shovel that turns over rocks, and you find things underneath.”
At the same time, the new work is raising unsettling questions about how to regard experimental results in a discipline for which rigorous proof is the gold standard.
At a workshop late in March in Oakland, Calif., mathematicians gathered to discuss current efforts in computer-assisted research and to consider the approach’s promise for the future. The workshop’s organizers, David Bailey of Lawrence Berkeley (Calif.) National Laboratory and Jonathan Borwein of Dalhousie University in Halifax, Nova Scotia, argue that computer experimentation is launching a new epoch in mathematics.
Computer power, Borwein says, is enabling mathematicians to make a quantum leap akin to the one that took place when Leonardo of Pisa introduced Arabic numerals—1, 2, 3, . . .—to European mathematicians in the 12th century.
“I have some of the excitement that Leonardo of Pisa must have felt when he encountered Arabic arithmetic. It suddenly made certain calculations flabbergastingly easy,” Borwein says. “That’s what I think is happening with computer experimentation today.”
Experimenters of old
In one sense, math experiments are nothing new. Despite their field’s reputation as a purely deductive science, the great mathematicians over the centuries have never limited themselves to formal reasoning and proof.
For instance, in 1666, sheer curiosity and love of numbers led Isaac Newton to calculate directly the first 16 digits of the number pi, later writing, “I am ashamed to tell you to how many figures I carried these computations, having no other business at the time.”
Carl Friedrich Gauss, one of the towering figures of 19th-century mathematics, habitually discovered new mathematical results by experimenting with numbers and looking for patterns. When Gauss was a teenager, for instance, his experiments led him to one of the most important conjectures in the history of number theory: that the number of prime numbers less than a number x is roughly equal to x divided by the logarithm of x.
Gauss often discovered results experimentally long before he could prove them formally. Once, he complained, “I have the result, but I do not yet know how to get it.”
In the case of the prime number theorem, Gauss later refined his conjecture but never did figure out how to prove it. It took more than a century for mathematicians to come up with a proof.
Like today’s mathematicians, math experimenters in the late 19th century used computers—but in those days, the word referred to people with a special facility for calculation. These specialists would often spend days or months making enormous tables of computations. Mathematicians of the time also built expensive three-dimensional geometric models to try to bolster their insight about solid geometry.
Today, electronic computers take only seconds to carry out calculations and to create beautiful graphics of three-dimensional shapes. Whereas Newton labored to calculate 16 digits of pi, for instance, the current computer-assisted record is more than 1 trillion digits (MathTrek, Science News Online: A Trillion Pieces of Pi).
David Mumford, a mathematician at Brown University in Providence, R.I., says that he tells his students that merely “having Excel software on their desktops gives them power that mathematicians in the past would have drooled over.” That power is now enabling researchers to discover hidden corners of the mathematical universe, many of which earlier mathematicians never dreamed existed.
Relating to pi
In 1995, Bailey used computer experimentation to discover something very much in the spirit of earlier experimenters. It was a new formula for pi (MathTrek, Science News Online.). Over the centuries, mathematicians have found many amazingly simple ways to express pi as an infinite sum. For instance, pi/4 = 1 – 1/3 + 1/5 – 1/7 + 1/9 . . . .
Bailey’s collaborators Peter Borwein of Simon Fraser University in Burnaby, British Columbia, and Simon Plouffe, now at the University of Québec in Montreal, had recently noticed that the logarithm of 2 has a simple infinite-sum formula with an unusual property. The formula can reveal, say, the millionth binary digit of log 2 with no need to calculate the 999,999 digits before it. Peter Borwein and Plouffe realized that about 20 other mathematical constants have similar shortcut formulas.
Together with Bailey, the pair wondered whether pi also has a shortcut formula. A thorough search of the mathematical literature failed to turn up any such formula.
“At the time, it seemed extremely unlikely to us that such a formula existed,” Bailey says. “We presumed that if it did, it would have been discovered 200 or 300 years ago.”
Nevertheless, the researchers decided to use a computer program designed by Bailey and Helaman Ferguson, a sculptor and mathematician based in Laurel, Md., to seek numerical relationships between pi and the constants the math team already knew to have shortcut formulas (MathTrek, Science News Online: Jazzing Up Euclid’s Algorithm). If they could find a relationship of the right kind—one that represented pi as a sum of the other constants multiplied by whole numbers—they knew they could use the known shortcut formulas to write a shortcut formula for pi.
The researchers calculated pi and the other constants to an accuracy of several hundred digits and set the computer searching for a relationship among these long strings of digits. Eventually, the computer found an equation that related pi to log 5 and two other constants.
Bailey recalls, “After months of runs with different constants, in the middle of the night, the computer found the relation, and it sent Peter and Simon an e-mail. The next morning, they wrote it out, and, sure enough, it gave a formula for pi.”
Once the computer had produced the formula, proving that it was correct was embarrassingly easy, Bailey says. “The proof is literally a six-line exercise in freshman calculus,” he explains.
This is frequently the case with experimental results, Jonathan Borwein says. “Often, knowing what is true is 99 percent of the battle,” he notes.
Knotty shapes
It might seem that computers’ calculating power makes them particularly well suited for tackling numerical questions rather than geometric ones. However, computer experimentation has also become a valuable tool for geometry.
Sophisticated software packages can perform complicated geometric calculations and produce shapes and patterns that mathematicians had never before visualized.
One program called SnapPea—created by Jeffrey Weeks, a freelance mathematician in Canton, N.Y.—has revolutionized the study of three-dimensional shapes with hyperbolic geometry, an alternative geometry to the one that Euclid compiled and most schoolchildren still study. Last spring, for example, Colin Adams, a mathematician at Williams College in Williamstown, Mass., used SnapPea to discover an unexpected property of certain knots.
Adams was interested in what mathematicians call knot complements: the three-dimensional shapes left behind when a knotted loop is drilled out of three-dimensional space, like a wormhole through an apple (SN: 12/8/01, p. 360). Mathematicians have known for decades that many knot complements have hyperbolic geometry.
One of the ways that mathematicians study such a shape is to examine a pattern of balls, called horoballs, that encodes the symmetries of the shape. While using Snappea to draw the horoball patterns corresponding to certain knots, Adams and his student Eric Schoenfeld stumbled upon something they had never seen before. It was a knot whose horoballs lined up into perfectly straight chains. Normally, the pattern of horoballs is random—”a mess,” Adams says.
“We thought, ‘That’s weird,'” Adams recalls. “It was really exciting.”
He and Schoenfeld eventually realized that the straight lines of horoballs indicated that the knot complement contains a special surface that is completely flat from the perspective of hyperbolic geometry. Previously, Adams says, mathematicians had no reason to expect such a surface to exist. After looking at more examples, Adams and several of his students proved that a whole family of knots has such surfaces.
“There’s no way we would have been led to these results without the computer,” Adams says. SnapPea has become an indispensable tool for studying shapes with hyperbolic geometry, he adds.
“I’m incredibly dependent on it and use it all the time as my laboratory,” he says. “These patterns just pop out at you that you have no explanation for, and then slowly you explain what you see.”
Modern three-dimensional hyperbolic geometry actually owes its origins to computer experiments, Adams says. It was through experiments by the late mathematician Robert Riley that William Thurston of Cornell University first realized in the 1970s that knot complements can have hyperbolic geometry.
Subsequent experiments led Thurston to formulate a famous conjecture about the kinds of geometry three-dimensional shapes can have—work that earned Thurston a Fields Medal, the highest honor in mathematics. Last year, Russian mathematician Grigory Perelman made headlines with a claimed proof of Thurston’s conjecture, which mathematicians are now scrutinizing (SN: 6/14/03, p. 378).
“Without the computer, this field of mathematics wouldn’t exist,” Adams says. Computers have “allowed us to explore areas of math we couldn’t explore before,” he says.
Paths to enlightenment
Although Adams worked out formal proofs to back up his experimental findings in hyperbolic geometry, computer experiments often lead mathematicians to findings that they have no idea how to prove.
“One thing that’s happening is you can discover many more things than you can explain,” Jonathan Borwein says.
If experimental discoveries indeed flood in faster than they can be proved, could that change the very nature of mathematics? In their book Mathematics by Experiment (2003, A K Peters), Bailey and Jonathan Borwein advance the controversial thesis that mathematics should move toward a more empirical approach. In it, formal proof would not be the only acceptable way to establish mathematical knowledge.
Mathematicians, Bailey and Borwein argue, should be free to work more like other scientists do, developing hypotheses through experimentation and then testing them in further experiments. Formal proof is still the ideal, they say, but it is not the only path to mathematical truth.
“When I started school, I thought mathematics was about proofs, but now I think it’s about having secure mathematical knowledge,” Borwein says. “We claim that’s not the same thing.”
Bailey and Borwein point out that mathematical proofs can run to hundreds of pages and require such specialized knowledge that only a few people are capable of reading and judging them.
“We feel that in many cases, computations constitute very strong evidence, evidence that is at least as compelling as some of the more complex formal proofs in the literature,” Bailey and Borwein say in Mathematics by Experiment.
Gregory Chaitin, a mathematician at IBM’s T.J. Watson Research Center in Yorktown Heights, N.Y., argues that if there is enough experimental evidence for an important conjecture, mathematicians should adopt it as an axiom. He cites the Riemann hypothesis. This conjecture postulates that, apart from a few well-understood exceptions, all the solutions to a certain famous equation have a simple relationship to one another.
Mathematicians have calculated billions of solutions to the equation, and they do indeed satisfy the relationship. On the basis of this evidence, Chaitin says, a physicist would accept the Riemann hypothesis and its far-reaching ramifications.
“Mathematicians have to start behaving a little more like physicists,” he says. “So many useful results are being suggested by experimental data that it seems almost criminal to say that we’re going to ignore the data because we have no proof.”
This view is far from mainstream, however. To Bernd Sturmfels, a mathematician at the University of California, Berkeley who does computer experiments in algebra, rigorous proof is precisely what distinguishes mathematics from physics.
“I think proof is very much at the heart of mathematics,” he says. “Our understanding can be significantly advanced by experiments, but I think there will always be a clear borderline as to what constitutes an acceptable result in pure mathematics.”
Mumford agrees. “I am quite certain that the psychology of pure mathematicians is different from that of scientists—that this idea of proof is central and will not be altered,” he says.
In the case of the Riemann hypothesis, mathematicians observe that although the experimental data may look convincing, other statements with similar amounts of supporting evidence have turned out to be false.
David Eisenbud, the director of the Mathematical Sciences Research Institute in Berkeley, Calif., points out that it wouldn’t further mathematicians’ understanding to accept the truth of a mathematical statement such as the Riemann hypothesis on the basis of computer-generated, experimental evidence. In contrast, the ideas in a proof might provide deep insight into why the statement should be true.
“Proof is the path to understanding,” Eisenbud says.
Regardless of whether mathematicians start behaving more like physicists, one thing seems clear. The crown jewel of the sciences finally has a lab instrument worthy of it.






